Shorのアルゴリズム入門
2019/06/21 マルゼミ 「Shorのアルゴリズム入門」概要
6/3のマルレク「暗号技術の現在」では、暗号技術が現在の「公開キー暗号/RSA暗号」から「ポスト量子暗号」に大きく変わろうとしているという話をしました。こうした変化を引き起こした最大の原因は、25年前に発見された「Shorの素因数分解アルゴリズム」です。
RSA暗号は、大きな素数p,q 二つの積である大きな数Nが、たとえNを知っていても、現在のコンピュータでは、その素因数p,qを求めることがとても難しいという事実をその基礎にしています。公開キー暗号は、コンピュータでも分解できないこのNを、事実上、皆の前に公開するという暗号方式です。Shorは「量子コンピュータを使えば」、Nの素因数分解が極めて高速に可能になることを発見しました。それは、「公開キー暗号/RSA暗号」が、簡単に破られるということを意味しています。
ではなぜ、こうした発見が25年間も「暗号技術に対する脅威」とは見なさなかったのでしょうか? その理由は簡単なものです。それは、「量子コンピュータ」が、すぐにも実現する技術とは見なされなかったからです。現時点でも、大きなNに対して、Shorのアルゴリズムでその素因数を求められる量子コンピュータは存在しません。
ただ、20年後40年後は、どうなっているでしょう?
近年になって、量子コンピュータの「実現可能性」について、大きな認識の変化があります。基本的には、いままでよりかつてなく多くの人が「いつか、確実な時期はわからないが、量子コンピュータは実現するだろう」と考えるようになってきました。Shorのアルゴリズムに対する関心が、新たに高まっているのは、そうした背景があります。NSAやNISTが、「ポスト量子暗号」への動きを本格化しているのは、当然のことだと思います。
本セミナーでは、Shorのアルゴリズムの概略を初等的に解説します。次のような話をしようと思います。
- 量子コンピュータではなぜ高速な計算ができるのか?
量子コンピュータでは、n個の入力に対して、その全ての状態の2^n個の「重ね合わせ」について同時並行的に計算ができます。普通のコンピュータと比較して「指数関数的」な高速化が可能となります。 - 量子コンピュータの出力は、どう取り出せるのか?
ところが、話はそう簡単ではありません。出力結果を取り出すということは、結果を観測することですが、観測したとたんに、量子の状態は、2^n個の重ね合わせの状態から、n個の状態のいずれかに変わってしまいます。これでは、せっかくの「重ね合わせ」による高速化の結果が台無しです。実は、入力についても、任意の量子状態を、あらかじめ準備するのは難しいのです。 - 量子の状態と「位相」
実は、例えば、二つの量子の状態 ( |0 + |1> )/√2 と( |0 − |1> )/√2 とは、明らかに異なる状態なのですが、観測によっては区別できません。|1>にかかっている +1, − 1 という係数を「位相」というのですが、異なっていても二乗して 1になるような位相を持つ量子の状態は、観測によっては区別できないのです。 - Shorのアルゴリズムと「位相」の評価
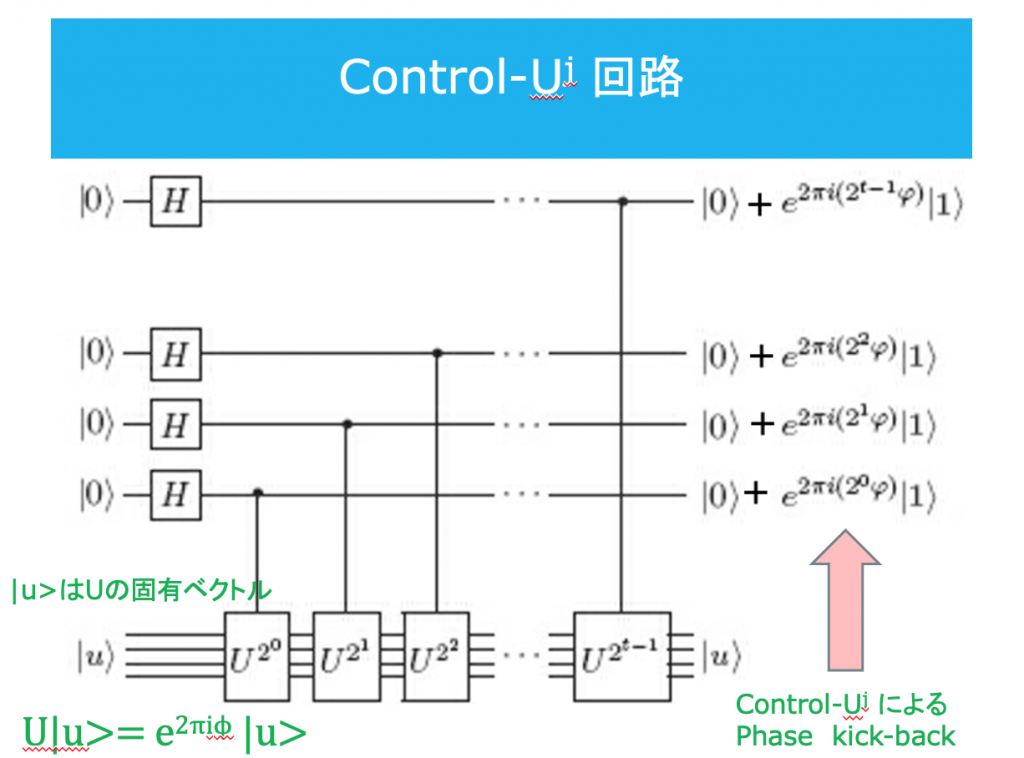
Shorのアルゴリズムというのは、量子コンピュータの超並列計算の能力を使って、バリバリと指数関数的な数の割り算をするアルゴリズムではないのです。その中心部分は、この「位相」の評価のアルゴリズムです。少し難しいのですが、セミナーではその概略を説明します。 - 「位相」の観測から、関数の「周期」を求める。
- 「周期」から、素因数を求める。
最後は、だいぶ省略しましたが、基本的な流れは、こういう感じです。
アルゴリズム、量子回路の細部は理解できなくとも、大まかなアルゴリズムの概略が説明できればと思います。それは、量子の世界の不思議な性質を知るいい機会になると思います。
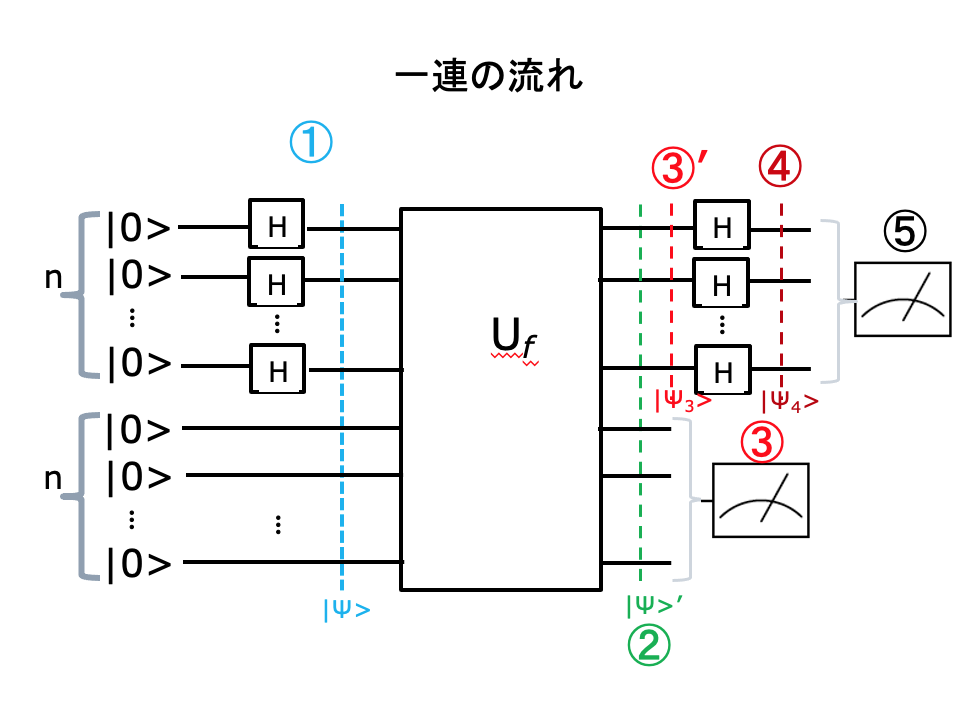
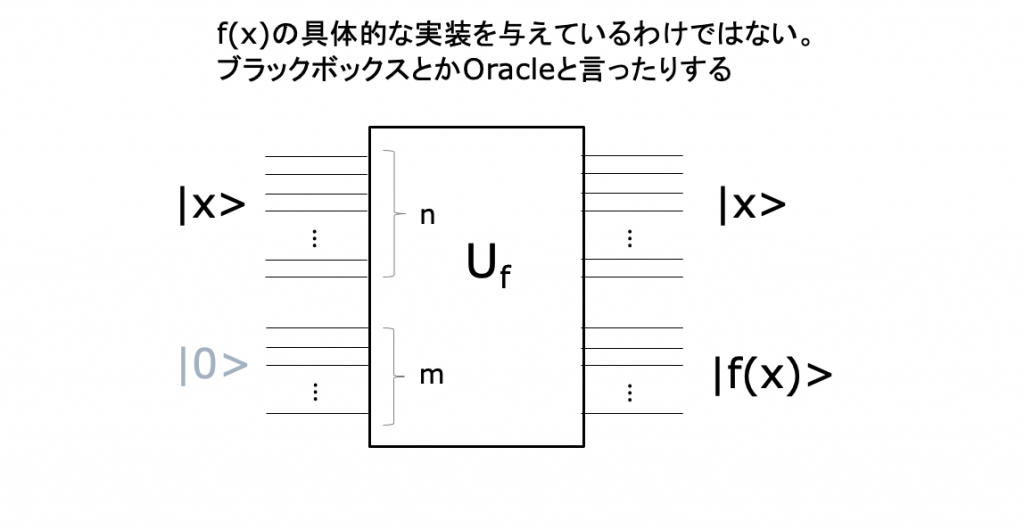
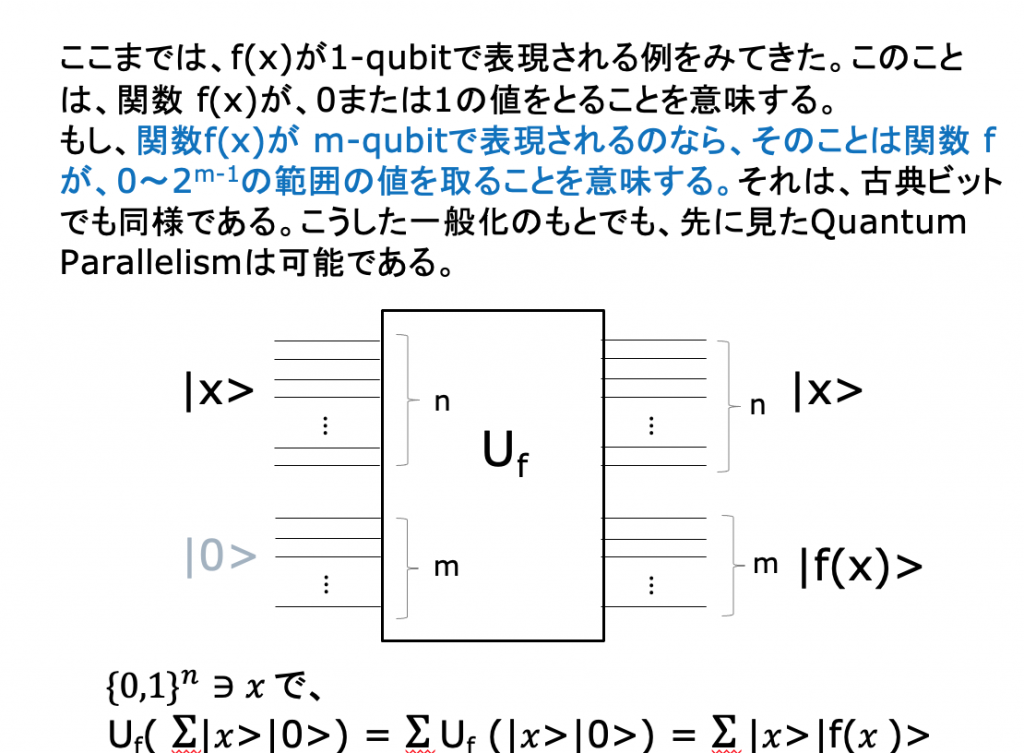
Part I : 任意のf(x)を計算する量子回路を考える
量子回路のユニタリ性
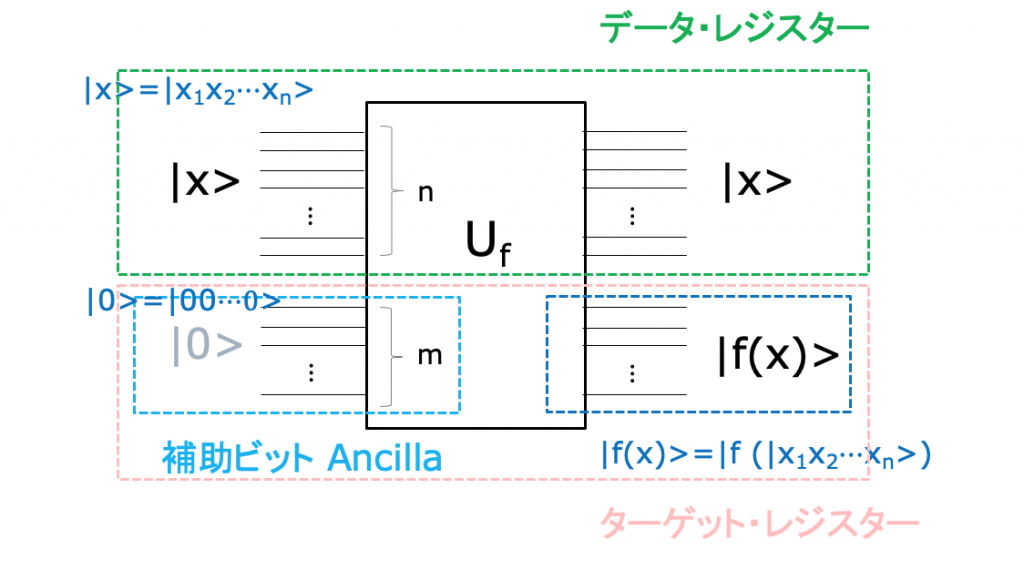
関数 f を計算する量子的なアルゴリズでも、入力 x のqubit数 n と、出力 f(x)のqubit数 m とは一般に独立である。
それでは、関数 f を計算する量子回路は、先の古典回路と同じような形を取るのだろうか? そうはならない。
量子ゲートはユニタリ変換を行うゲートなのだが、量子ゲートから構成される量子回路も、それ自体がユニタリ性を持たねばならない。量子回路全体に対応するユニタリ行列は、巨大なものになる。
例えば、2-qubitの入力を受け取り、2-qubitを出力する量子ゲート(CNOTがそうである)は、4次元のベクトルを受け取り、4次元のベクトルに変換する 4x4の行列で表現される。
n-qubitの入力を受け取り、n-qubitを出力する量子回路は、 2n x 2n のユニタリ行列で表現される。
量子回路の可逆性(reversibility)
回路全体を表現するユニタリ行列Uを書き下ろすことができないにしても、Uの性質 UU†=U†U=I から次のことがわかる。
回路U(行列Uに対応する)の入力と出力を入れ替えても、すなわち、Uに対するある入力|A>の結果であるUの出力|B>を、Uの出力側に与えても、Uは|A>を出力する。これを、量子回路の可逆性という。
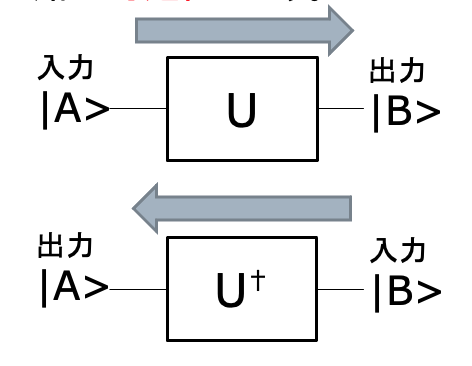
古典回路は非可逆である。任意の関数は、ユニタリでは表現できない
古典回路は、非可逆である。
また、任意の関数 f をユニタリ行列で表現できるわけではない。
例えば、f(x)=z, f(y)=z という関数 f がユニタリ行列で表現できたとする。これは、U|x>=|z>, U|y>=|z>を意味するのだが、両式を引くと U(|x>−|y>)=0 となるのだが、こうしたUはユニタリではない。
任意のf(x)を計算し、かつユニタリな量子回路Ufの一般的な形
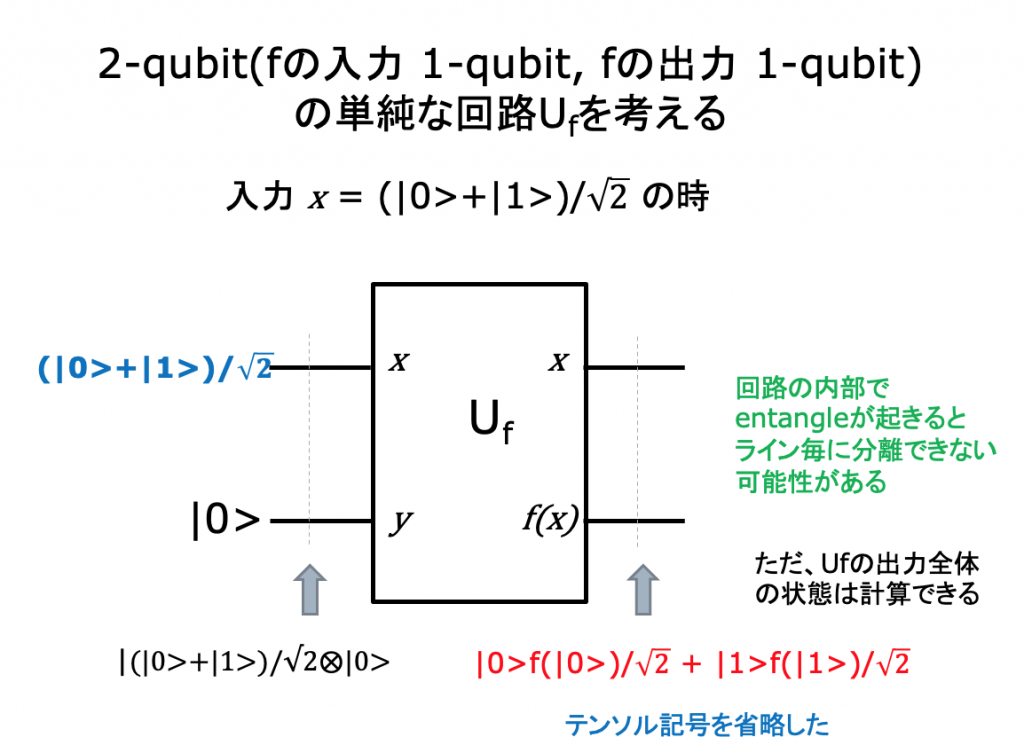
関数 f は線形であるとは限らないが、Ufはユニタリであり線形である。Mが線形であるとは、
M(a|A>+b|B>)=aM|A>+bM|B>が成り立つことをいう。 x = |0> の時と x = |1> の時の例から、Ufは次の式を満たすことがわかる。
Uf(|0>⨂|0>)= |0>⨂f(|0>)
Uf(|1>⨂|0>)= |1>⨂f(|1>)
この時、Ufは線形であるので、
Uf((|0>+|1>)/√2 ⨂|0>)
= Uf((|0>/√2 ⨂|0>+|1>/√2 "⨂|0>")
= Uf(|0>⨂|0>)/√2 + Uf(|1>⨂|0>)/√2
= |0>⨂f(|0>)/√2 + |1>⨂f(|1>)/√2
= |0>f(|0>)/√2 + |1>f(|1>)/√2
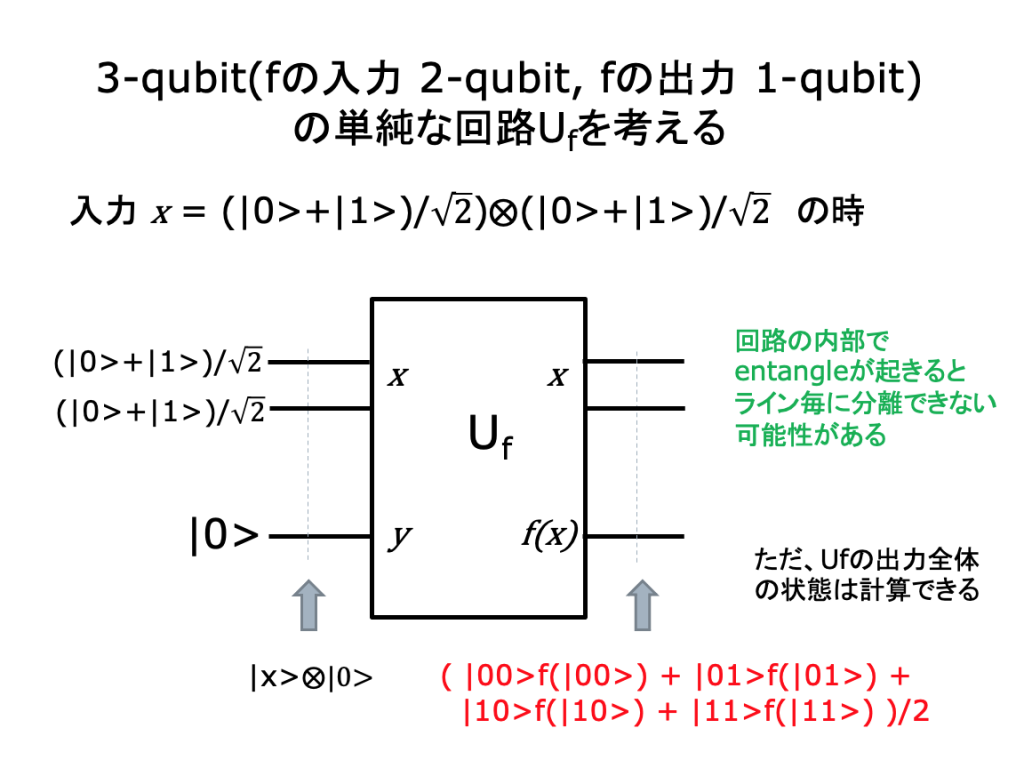
x = (|0>+|1>)/√2)⨂(|0>+|1>)/√2 とする。
x = (|00>+|01>+|10>+|11>)/2 である。
この時、
Uf(|x>⨂|0>)
= Uf((|00>+|01>+|10>+|11>)⨂|0>)/2
= (Uf(|00>⨂|0>)+Uf(|01>⨂|0>)+
Uf(|10>⨂|0>)+Uf(|11>⨂|0>))/2
= (|00>⨂f(|00>)+|01>⨂f(|01>)+
|10>⨂f(|10>)+|00>⨂f(|11>)/2
=( |00>f(|00>) + |01>f(|01>) +
|10>f(|10>) + |11>f(|11>))/2
Part I 講演資料 (ダウンロード)
Part II : Quantum Parallelism
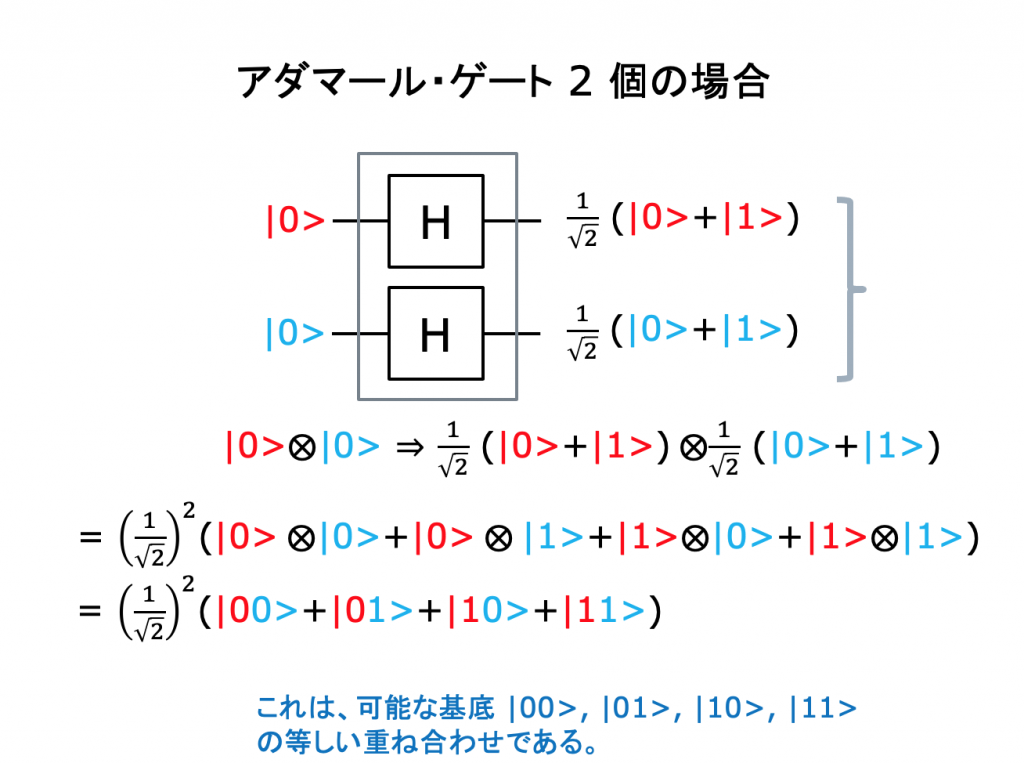
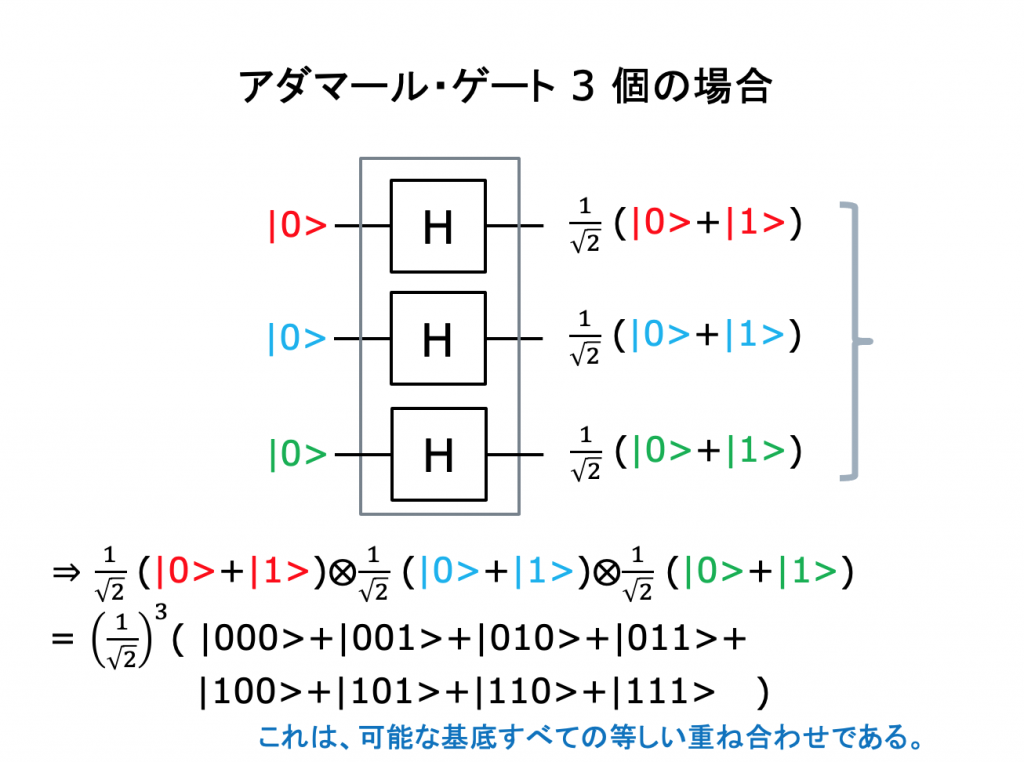
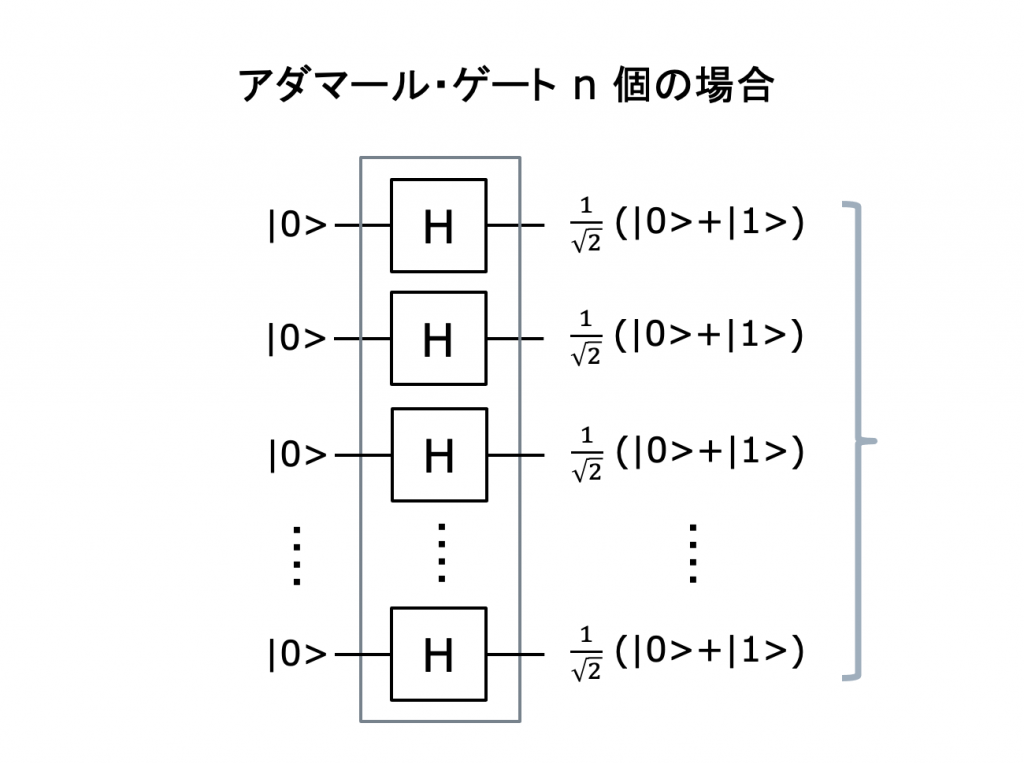
量子コンピュータではなぜ高速な計算ができるのか?
可能なすべての基底の等しい重ね合わせを作る

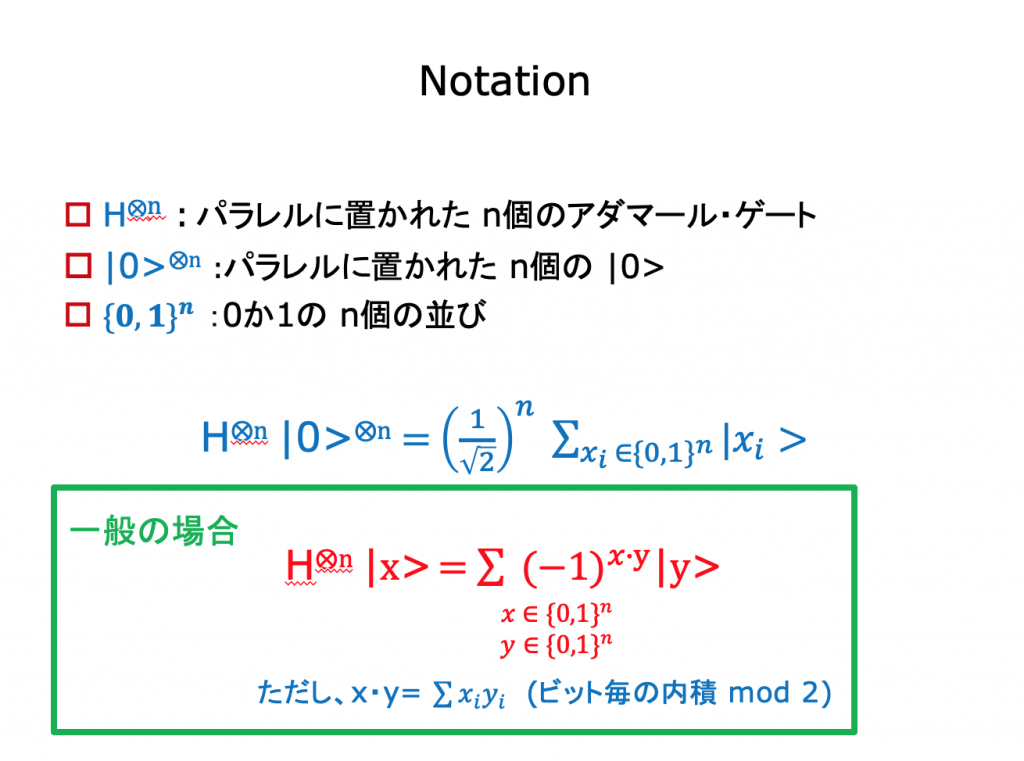
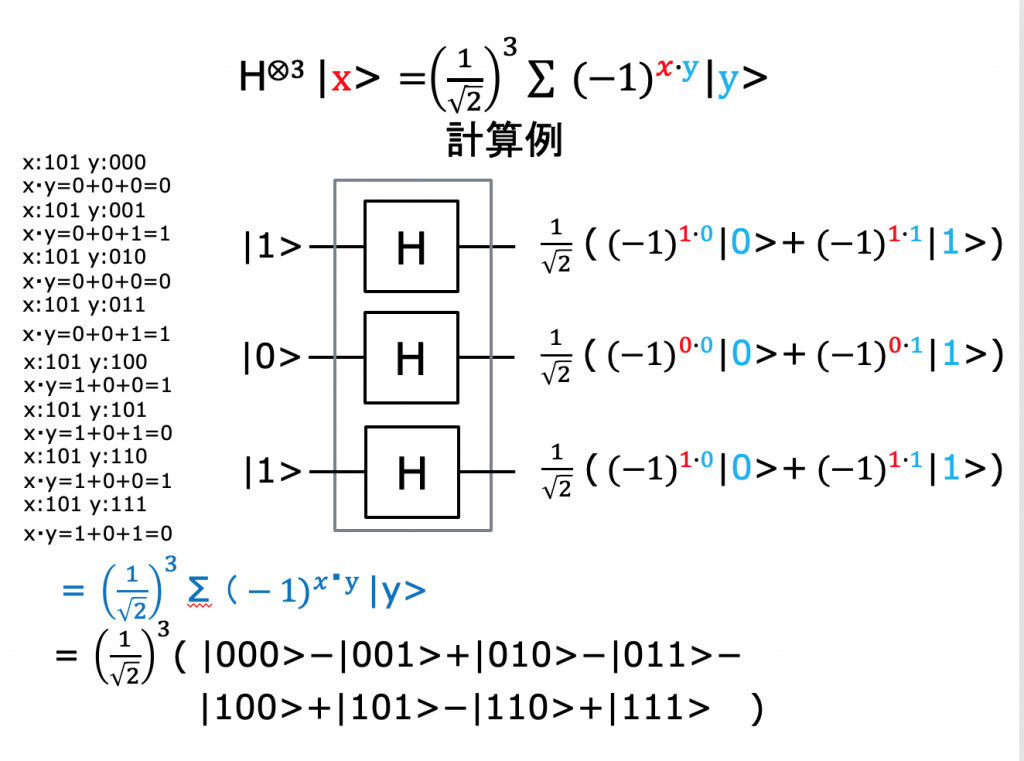
Quantum Parallelism
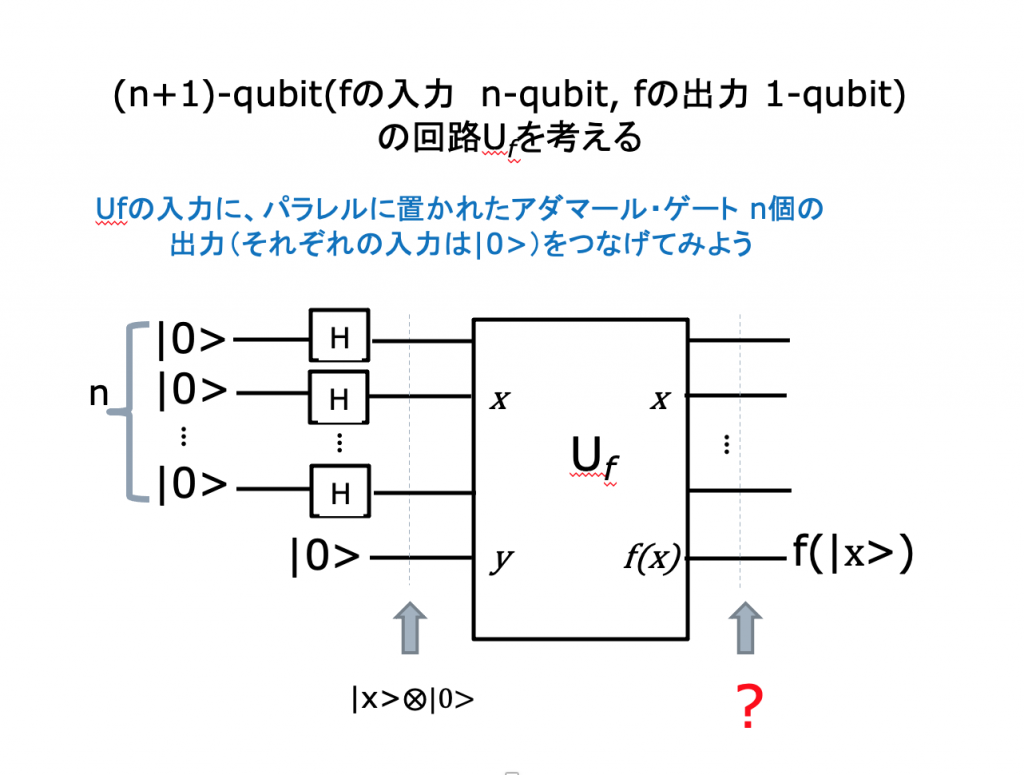


量子コンピュータの出力は、どう取り出せるのか?
出力を取り出す=出力を観測する
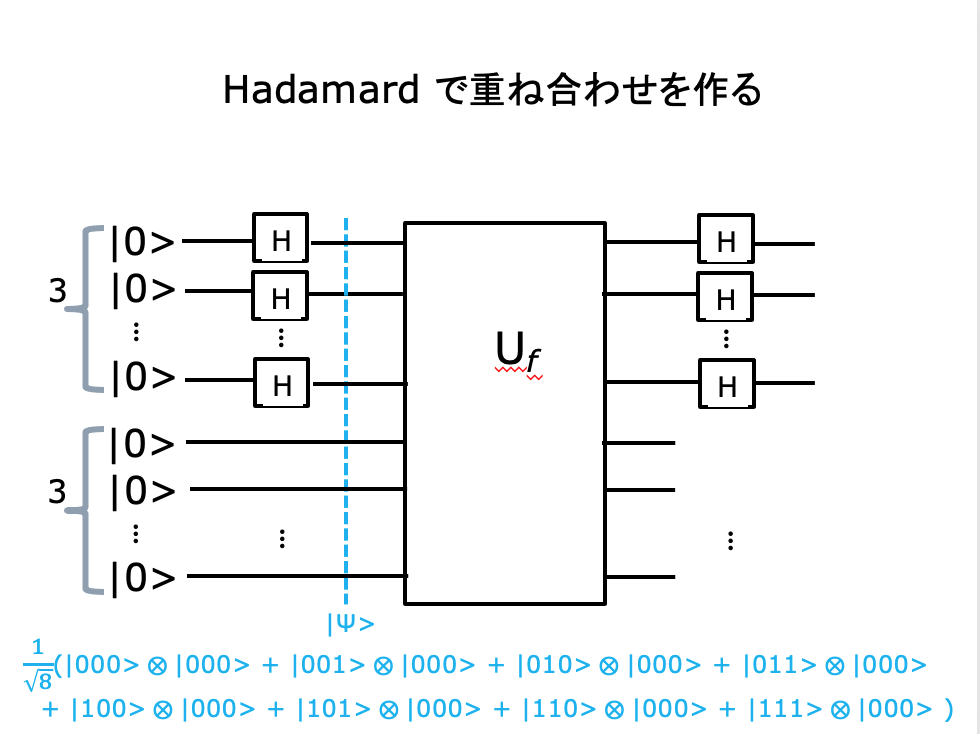
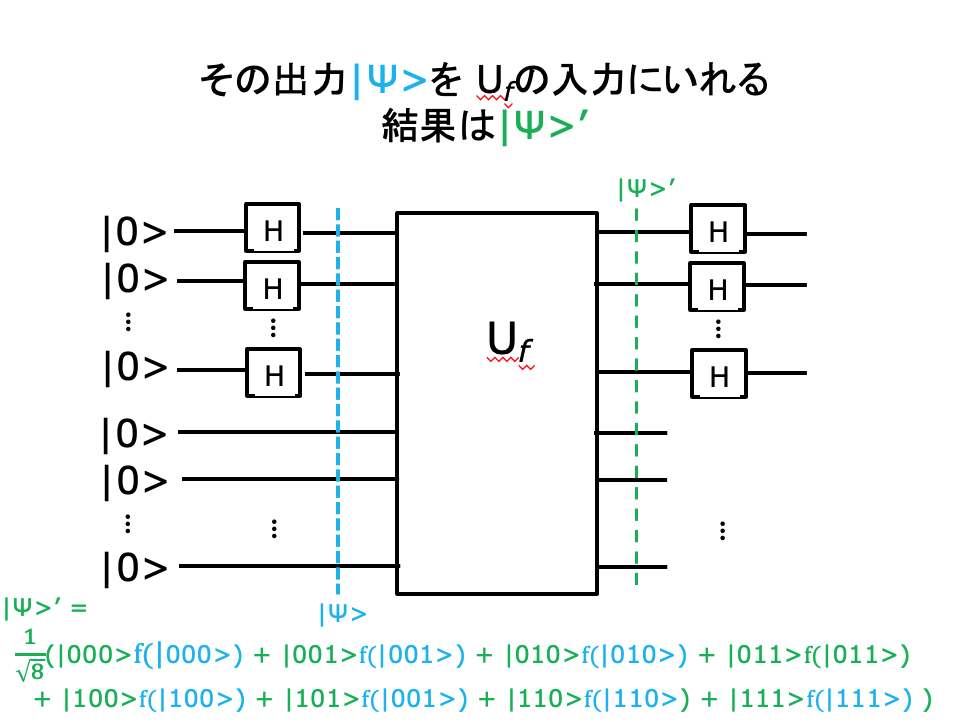
先のような回路を組めば、一回のUfの適用で出力側に〖{0,1}〗^𝑛 ∋𝑥 なるすべての𝑥について、Σ|𝑥>𝑓(|𝑥>) が現れるので、2n 回の f の計算ができるように見える。
ところが、話はそう簡単ではない。出力結果を取り出すということは、結果を観測することである。


Σ|x>f(|x>)の観測
重ね合わせの状態のΣ|x>f(|x>) を観測したとたんに、重ね合わせの状態は失われ、我々が観測するのは 個別の
|x>f(|x>)のみである。
例えば、n=3の時、Ufの出力が次のようになっていても、
(1/√2)^3(
|000>f(|000>)+|001>f(|001>)
+ |010>f(|010>)+|011>f(|011>)
+ |100>f(|100>)+ |101>f(|101>)
+ |110>f(|110>)+|111>f(|111>)
)
我々が観測できるのは、xの一つの値についての |000>f(|000>) または |001>f(|001>) または・・・ |111>f(|111>)のみである。

Part II 講演資料 (ダウンロード)
Part III : Simonのアルゴリズム
Simonの問題
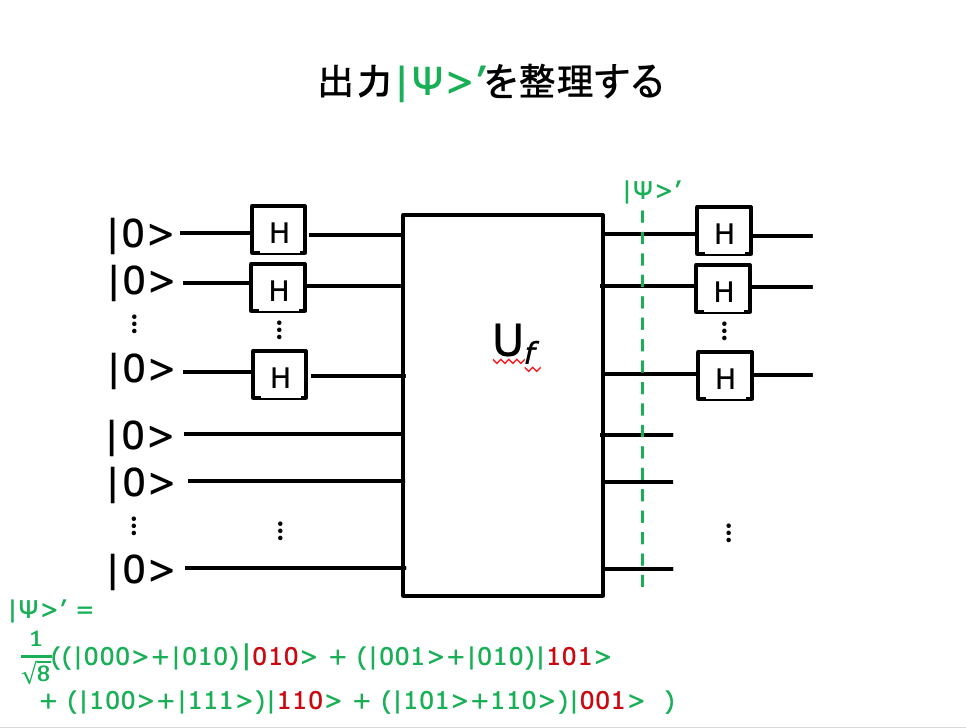
n-bitで表される整数からn-bitで表される整数への関数 fがあって、ある整数aについて f(x)=f(x⨁a) が成り立つという。この時、「周期」aを求めよという問題を、Simonの問題という。
x⨁a は、ビット列x とビット列a のビット毎の排他的論理和XORである。(対応するbitが同じなら0に、違っていたら1)例えば、 1101⨁1101=0000, 0000⨁1101=1101である。
この問題は、aとして全てのビットが0である 000…00 をとれば、 x⨁a=x ⨁ 0n =x となるので、自動的に満たされる。 (n個の0の並びを 0n と表している)
ただ、関数f によっては、a=0n以外にも、 f(x)=f(x⨁a) を満たすaが存在する場合がある。
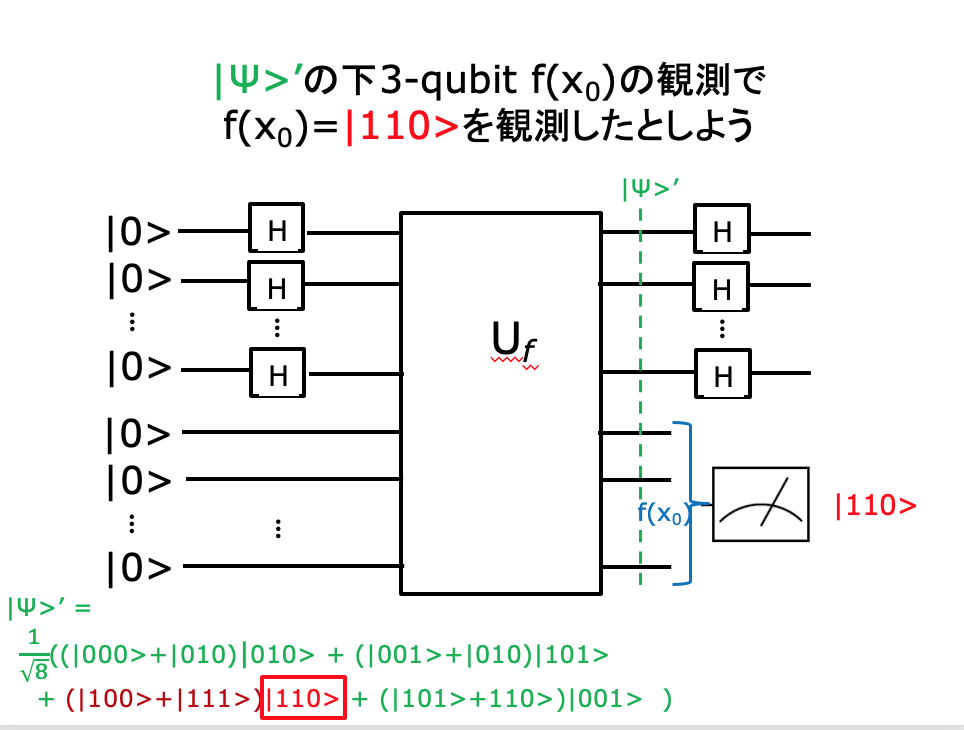
Simonの問題を解く回路
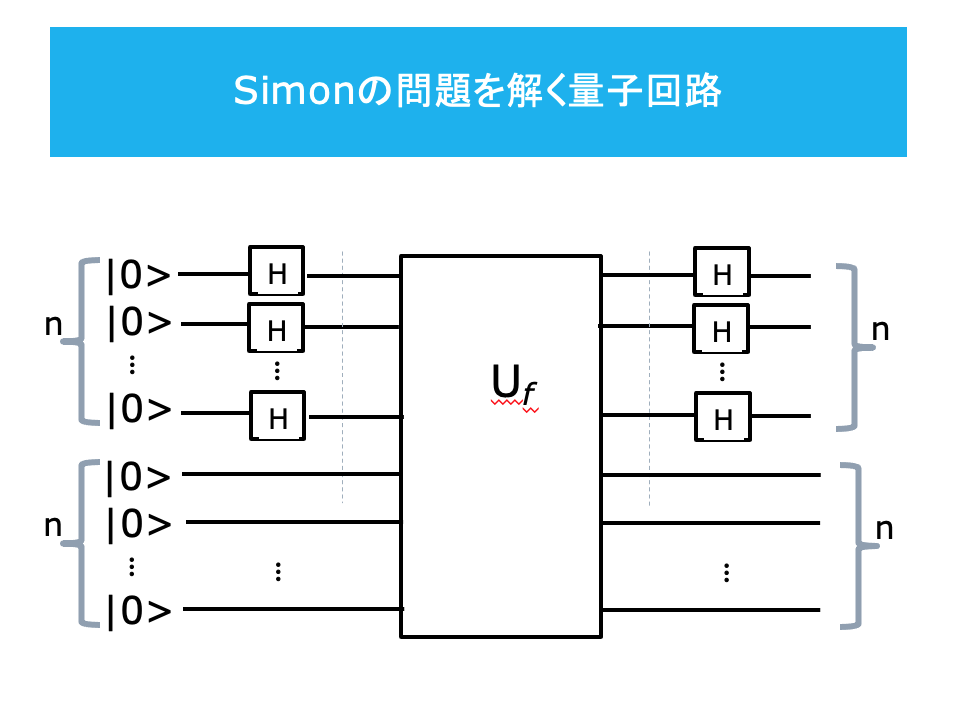
n=3 の場合の実行例
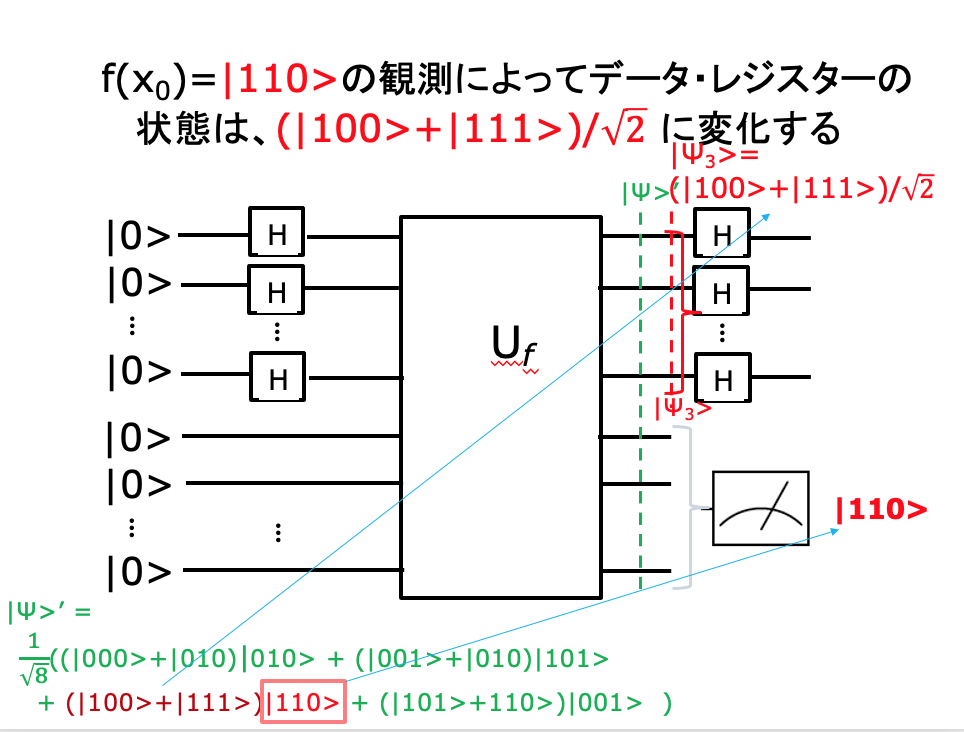

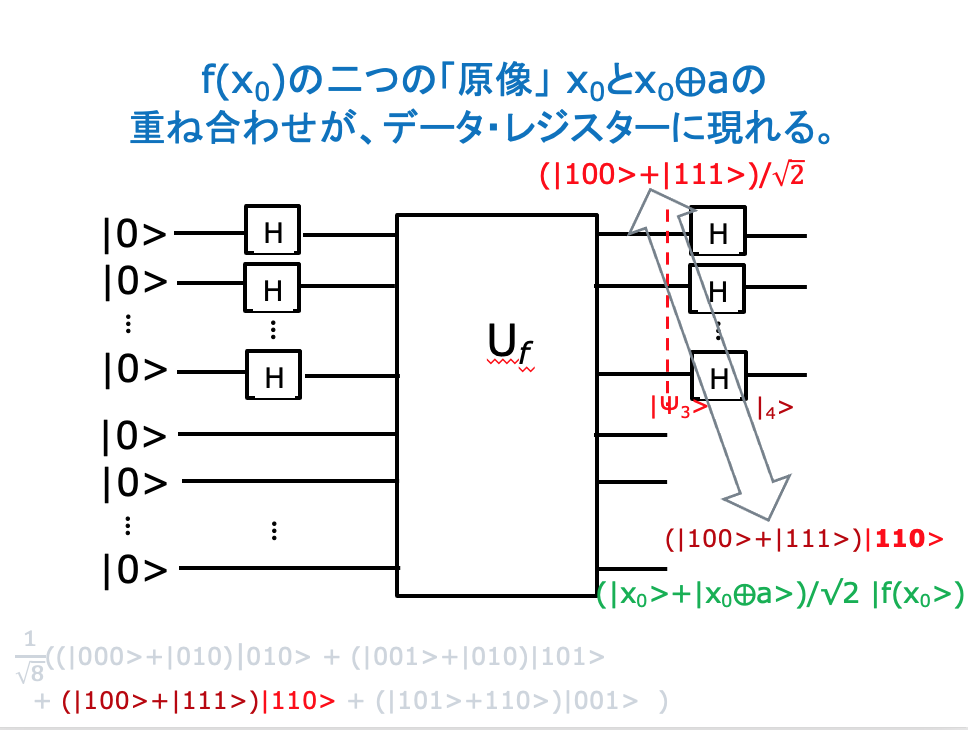


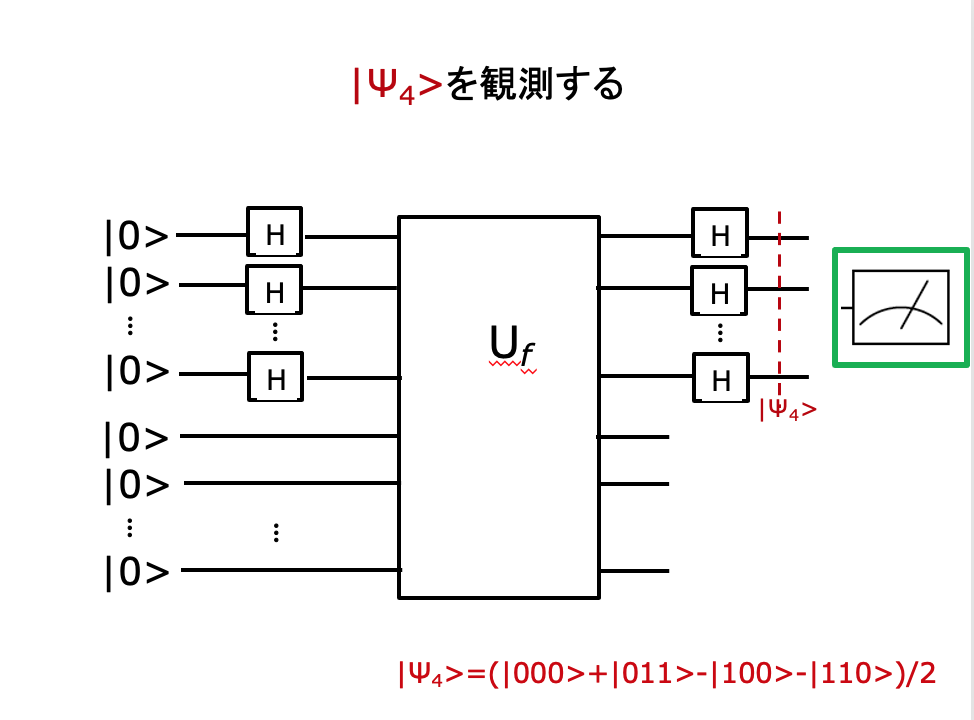

一般的な解法