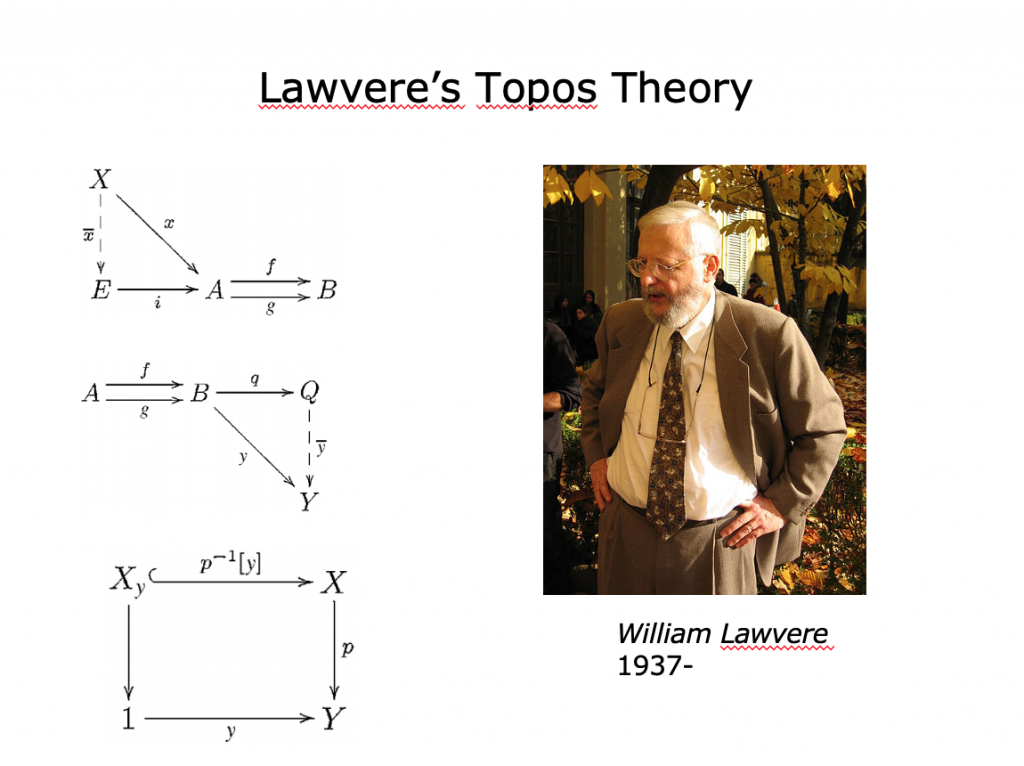
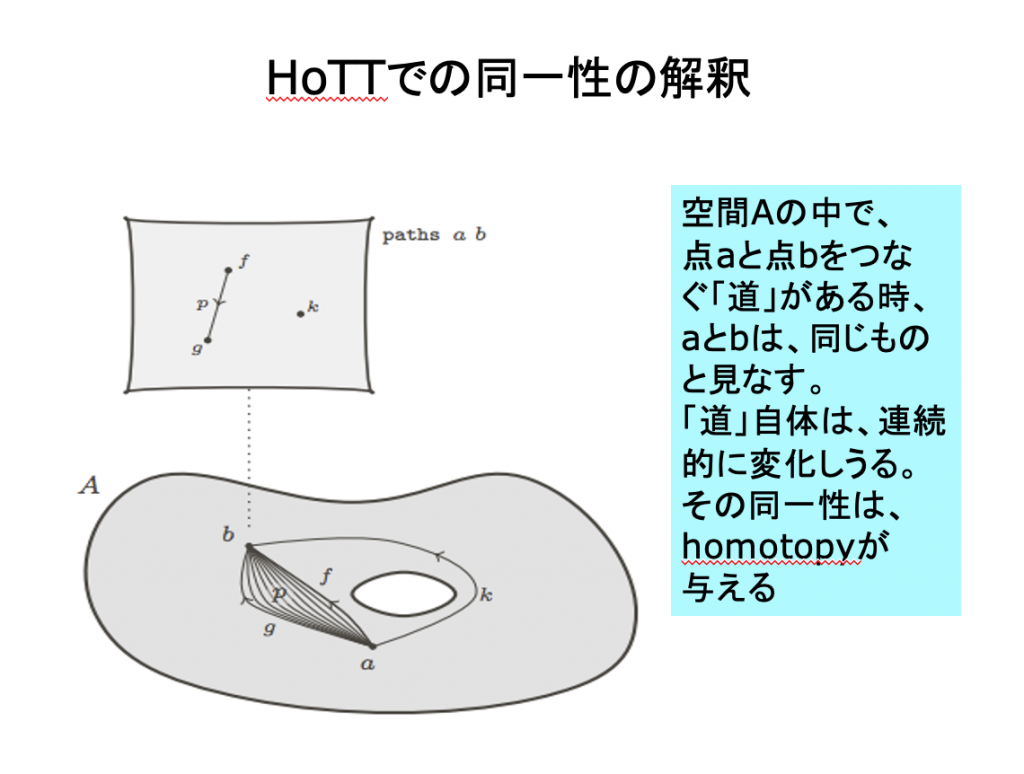
集合論入門

2018/05/29 MaruLabo数理ナイト「集合論入門」概要
集合論は、19世紀後半に、ドイツの数学者ゲオルグ・カントールが創り出した数学の一分野です。それまでの数学が、微分や積分や無限級数や幾何学的図形や物理的な運動を対象にしていたのに対して、集合論が対象とするのは、より抽象的な「集合」そのものです。その意味では、集合論の登場は、現代数学の一つの特徴である「抽象化」の歴史的な第一歩といっていいと思います。
ただ、集合論の基本的考え方は、決して抽象的なものではありません。それは、極めて具体的な、「集める」「数える」といった操作を基礎にしています。集合とは、いろいろなものを集めてできたものに、一つのまとまりを与えることです。逆に、いろんなもの(これを「要素」といいます)は、この集合に「属する」と考えます。
集合について大事な特徴の一つは、我々は、集合の要素の数を数えることができると言うことです。こうした考えは自然なもので、小学生に初めて足し算を教えるときには、この集合のモデルを使っています。「赤い石が三つのかたまりと、青い石が五つのかたまりを、一緒にすると、石はいくつ? 数えてみましょう。」
問題は、こうした素朴な考えを進めていくと、あるところで、急に難しくなるということです。集合論の創始者のカントールが考えた一番難しい問題の一つは、次のようなものでした。答えられますか?
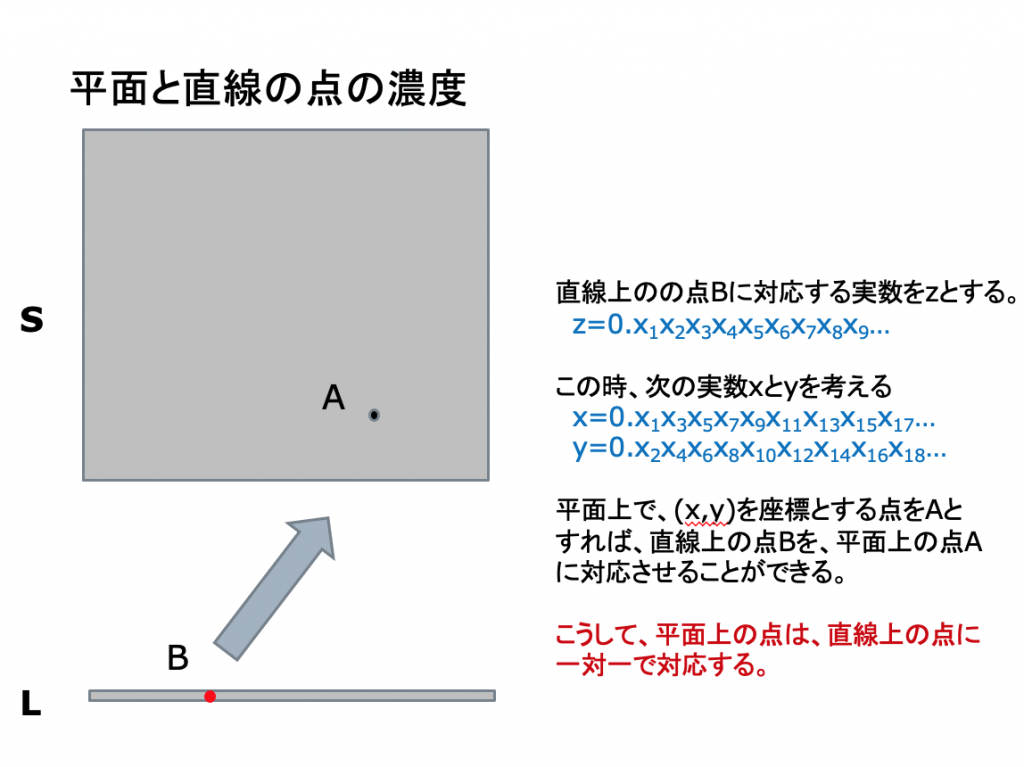
「線は、点を集めたもの。それでは、この線分の上に、点は何個あるのか数えてみよう。」
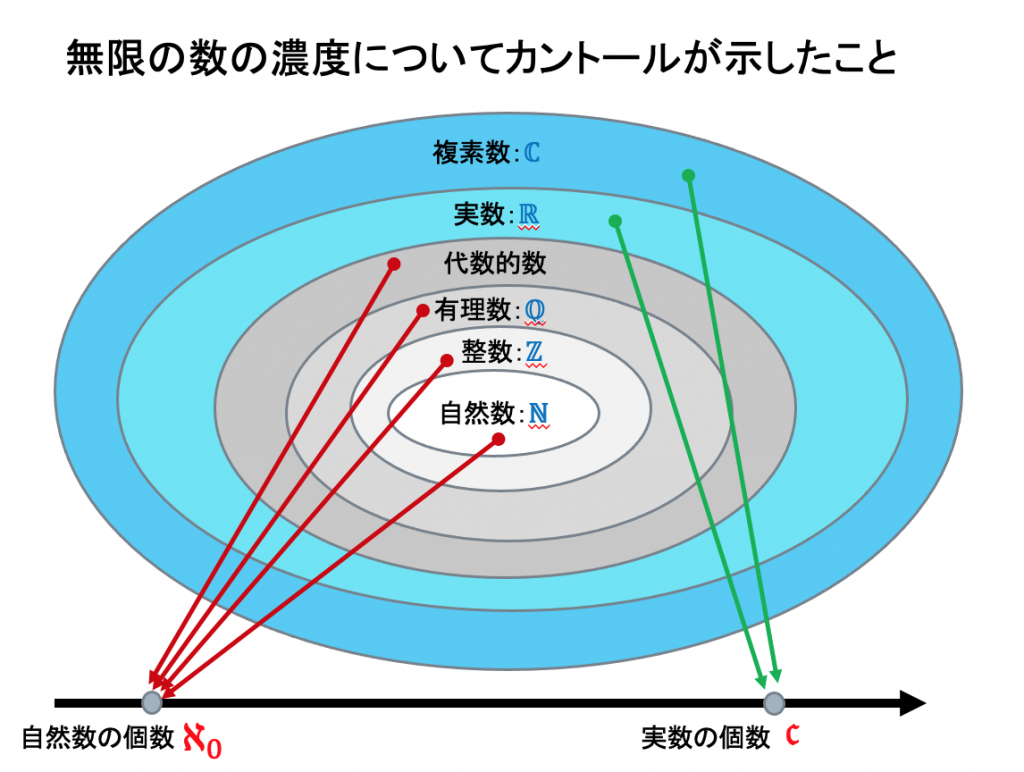
もちろん、線の上には、無限個の点が存在します。ただ、カントールは、驚くべきことを発見します。私たちに一番身近な無限の例は、1, 2, 3, 4, …. と無限続く自然数です。自然数は、無限個存在します。カントールは、線のように連続なもの(実数で表されます)の上の点の数は、自然数のなす無限より大きいことに気づきます。
無限は一つではないのです。実数の個数は、やはり無限なのですが、その無限は、自然数の個数の無限より大きいのです。
こうして、集合論は、主要に、無限と連続というものを数学的に考える数学として出発します。ただ、その前途は、平坦なものではありませんでした。
講演資料の構成
「数える」を考える

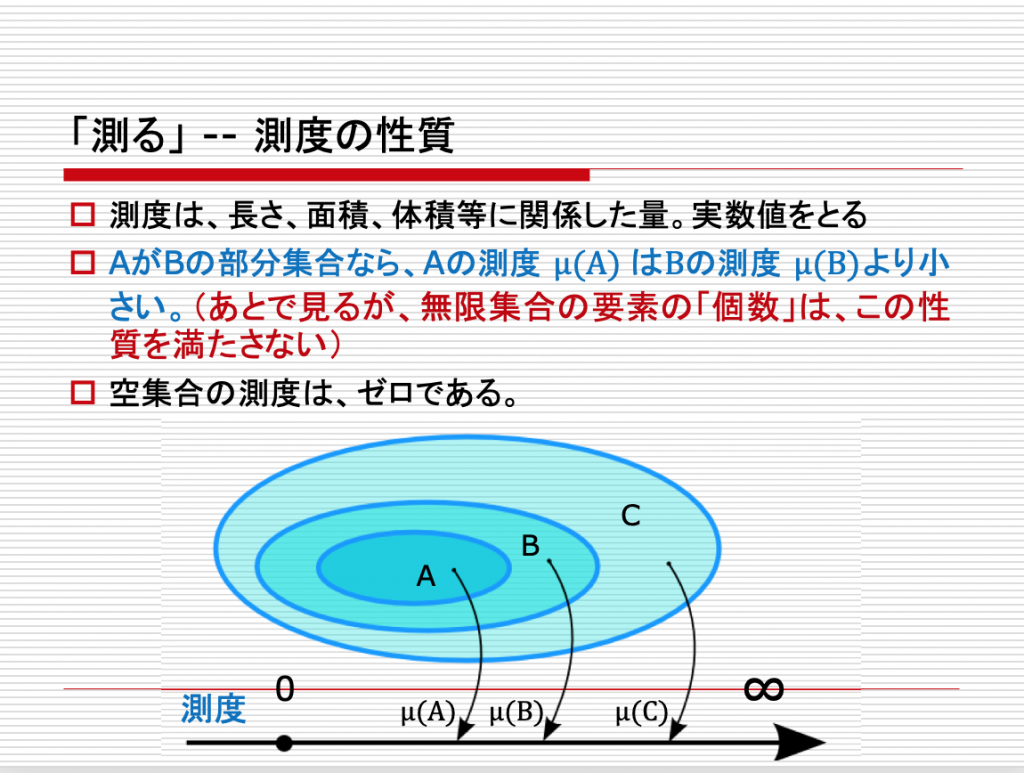
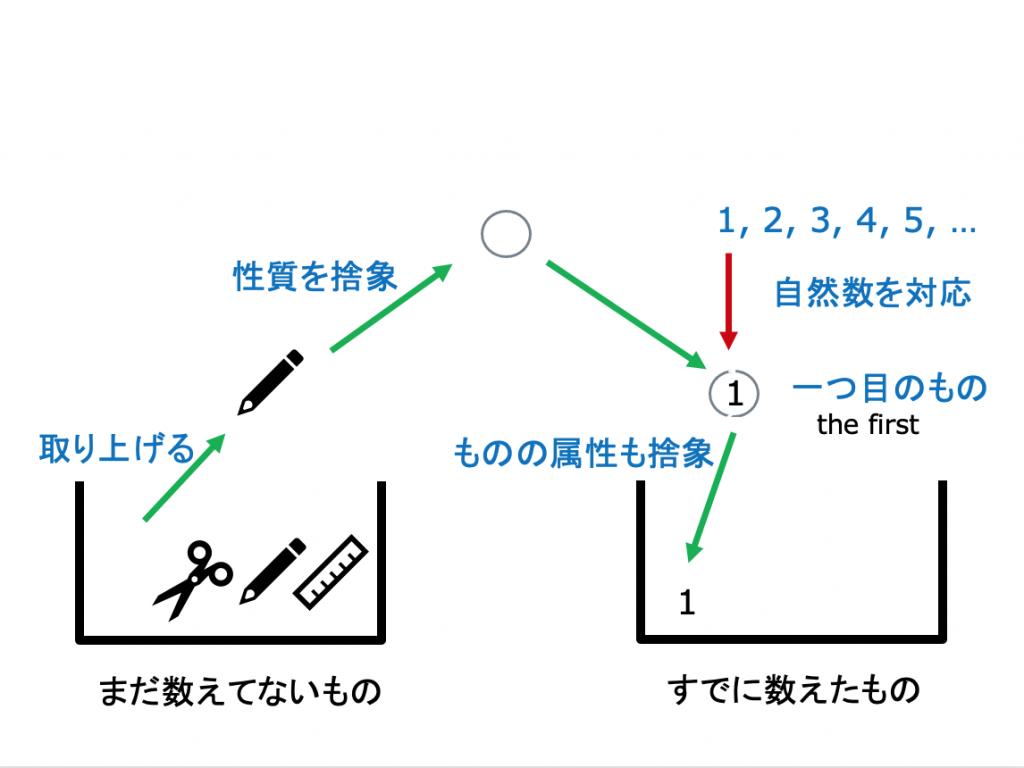
カントールの考えたこと 1 — 無限に数え続ける方法





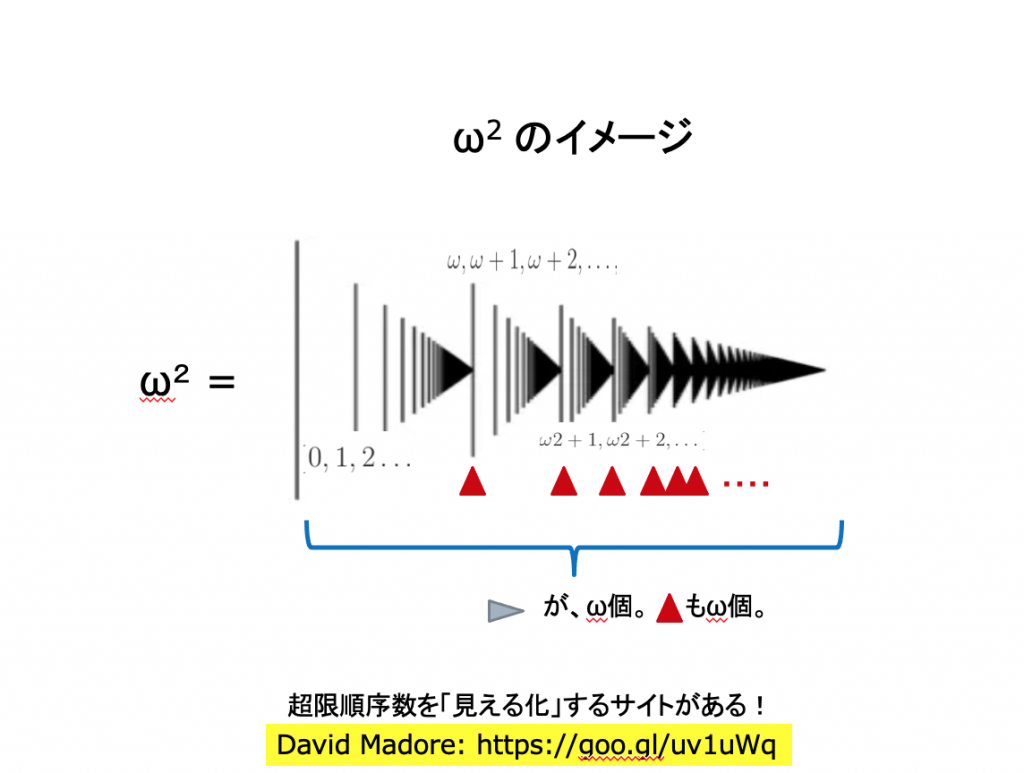

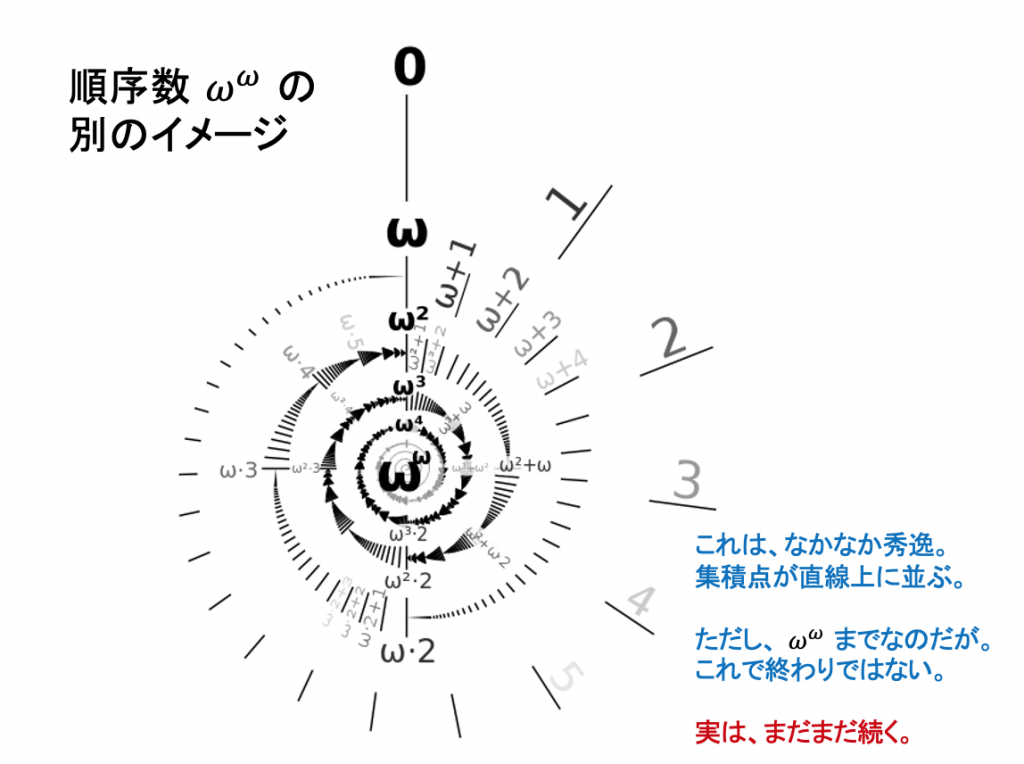
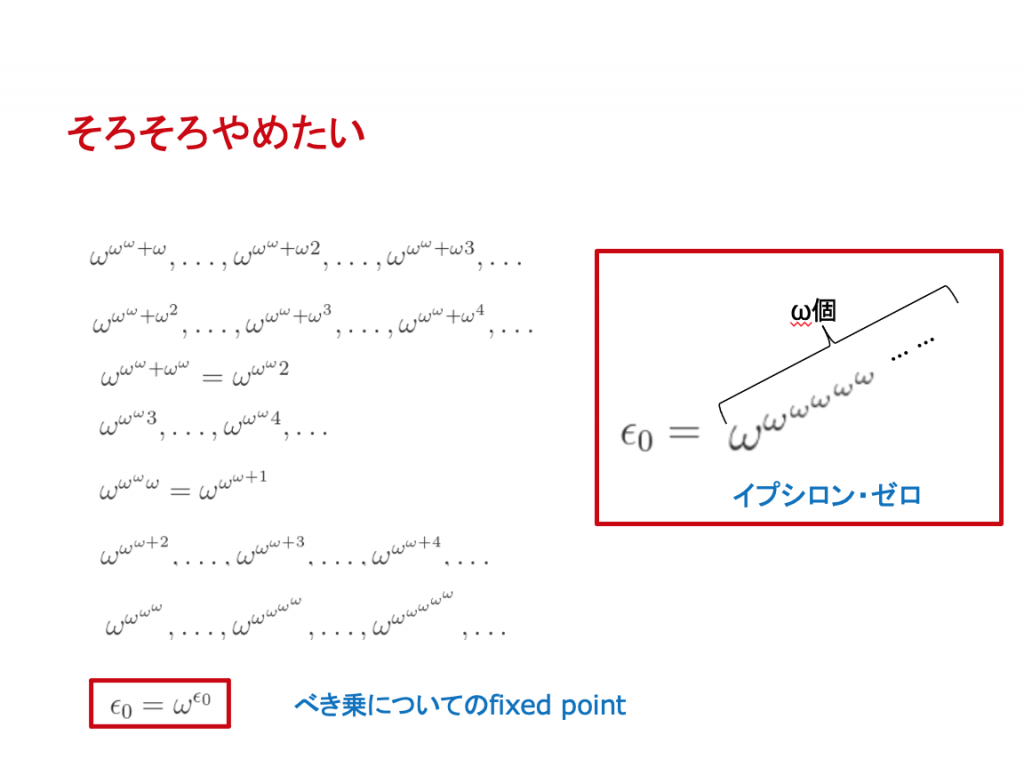
カントールが考えたこと 2 — 無限集合の要素の個数
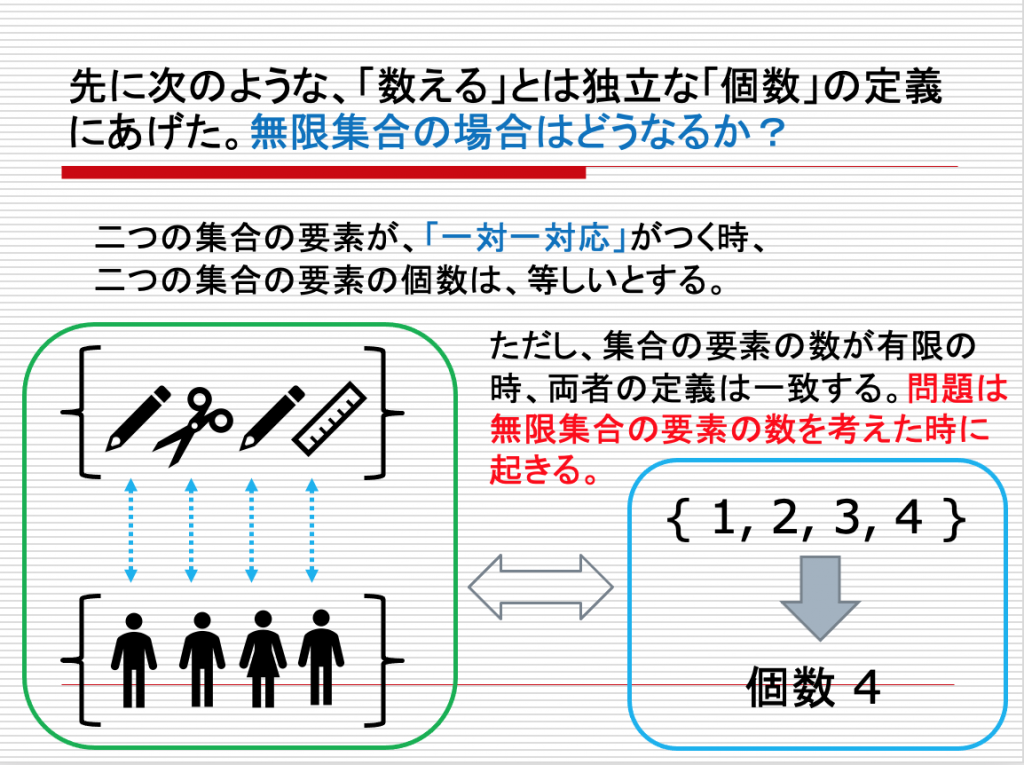




カントールが証明できなかったこと – 連続体仮説


集合論の体系の整備
ラッセルが見つけた集合論の矛盾
ZF: ツェルメロ=フランケルの公理的集合論
非カントール的集合論の発見
ゲーデル 1940年連続体仮説と集合論の無矛盾性の証明
コーエン 1963年連続体仮説と集合論の独立性の証明
数学の基礎を基礎付ける試みの発展