「プログラム と論理」関連ページ
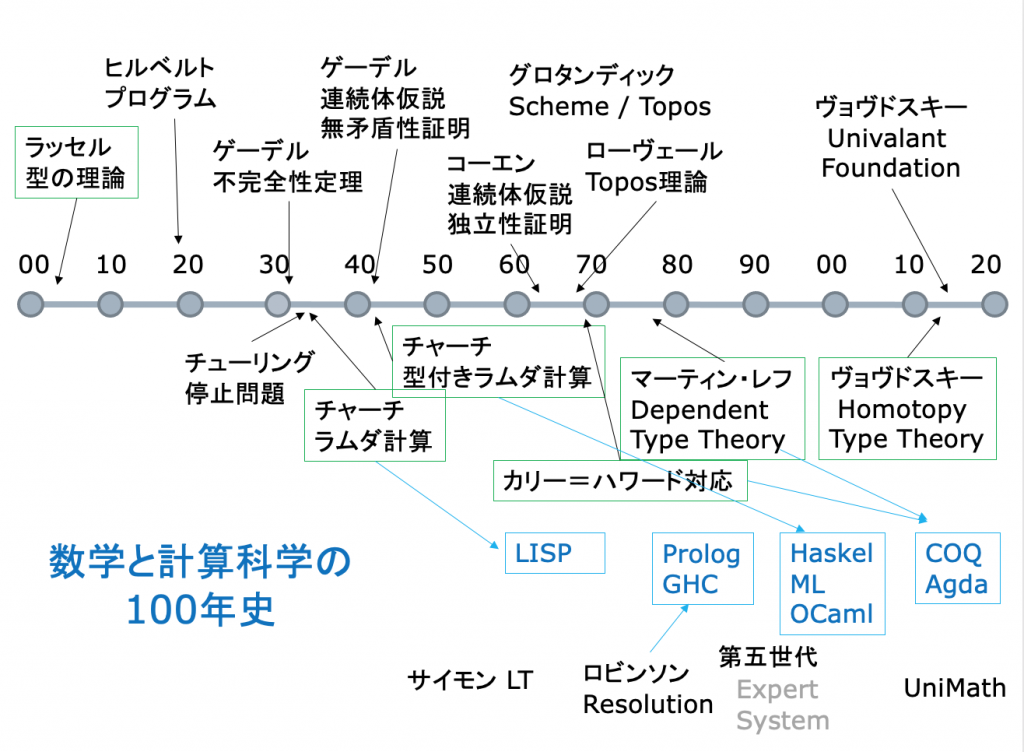
論理学と数学的証明
数理哲学への招待
数学を無味乾燥なつまらない学問だと思っている人は、少なくないと思います。大学受験の世界では、数学は、決して人気の科目ではありません。また、「数学なんて、生きていくのに役に立つの?」と「根本的」な疑問を持っている少年・少女達もたくさんいるでしょう。
今度のセミナーの目標は、数学が面白いことを感じてもらうというものにしようと思っています。
集合論入門
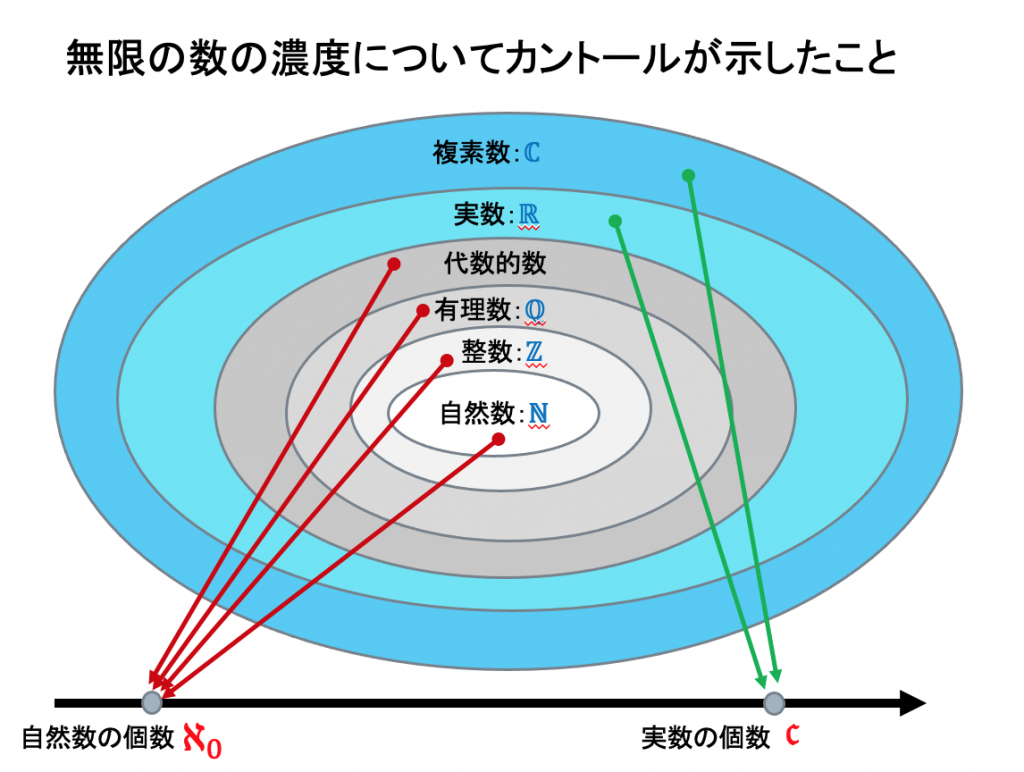
集合論は、19世紀後半に、ドイツの数学者ゲオルグ・カントールが創り出した数学の一分野です。
集合論の登場は、現代数学の一つの特徴である「抽象化」の歴史的な第一歩といっていいと思います。
集合論は、主要に、無限と連続というものを数学的に考える数学として出発します。ただ、その前途は、平坦なものではありませんでした。
論理学入門 I — 命題論理の演繹ルール
丸山は、人工知能技術の次の飛躍は、コンピュータの論理的に推論する能力が、現実の課題に広く応用される時に始まると考えています。
重要なことは、機械に論理的推論をさせるためには、我々が行う論理的推論が、どのようなルールに基づいているのかを意識的に捉える必要があるということです。論理学を学ぶことで、はじめて、その論理的推論のルールを学ぶことができます。
論理学入門 II — ラムダ計算と関数型言語
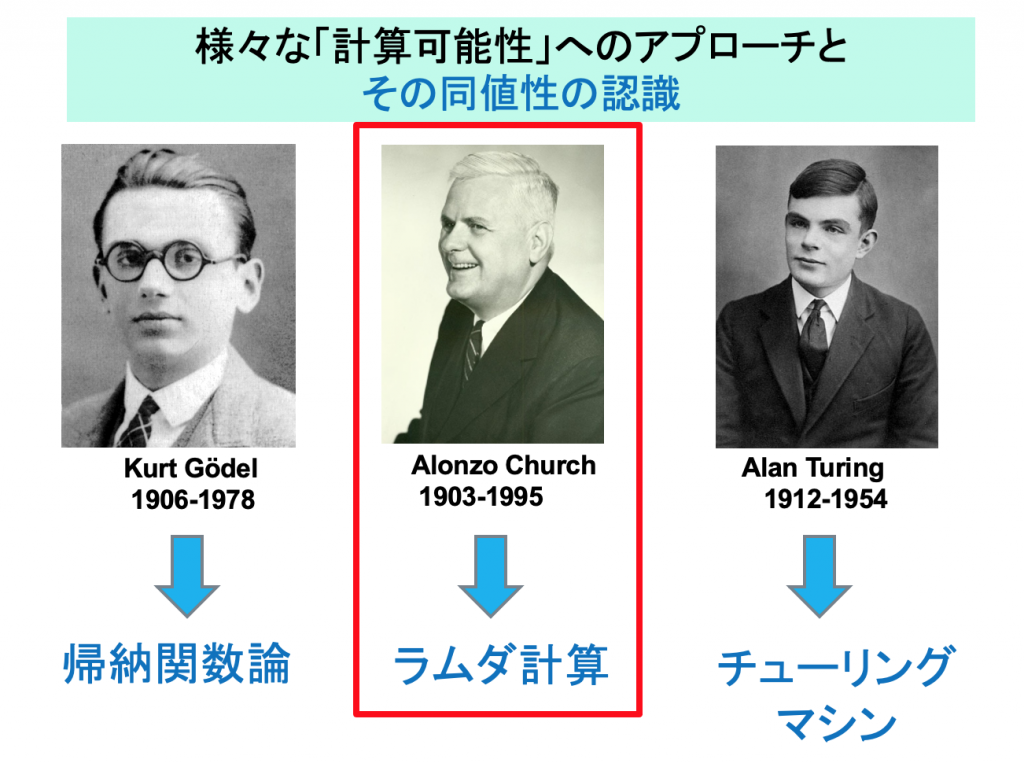
今回のセミナーでは、1930年代にチャーチが定式化した、「型のないラムダ計算」と同じくチャーチが1940年代に開発した、「型付きラムダ計算」を学びます。「型付きラムダ計算」は、現代の関数型言語の基礎になります。関数の型を含めて、型のチェックそのものが、プログラムの正しさの証明になるというのが、このセミナー・シリーズが志向する「論理・証明型言語」の基本的な考え方です。
論理学入門 III — 型の理論入門

「型の理論」は歴史的には、数学をどのように基礎づけるかという問題と結びついて発展してきました。同時に「型の理論」は、現代では、数学の基礎に対する関心とは、いわば正反対の、数学の実際的応用である計算機科学と密接に結びついています。
「型の理論」が明らかにした、「証明」=「計算」=「プログラム」という三位一体の関係の認識は、21世紀の計算科学の出発点になるべきものだと、僕は考えています。
「同じ」を考える — 「型の理論」入門

「同じ」あるいは「同じではない」という判断は、知覚にとっても認識にとっても、最も基本的な判断の一つである。認識の対象が、自然であれ、人間であれ、あるいは、思惟が産み出す抽象的な概念であれ、その認識の土台には、対象の「同一性」についての判断があるように思う。
セミナーでは、また、一昨年(2017年)急逝した数学者のVoevodskyの
「同一性」をキーコンセプトにした数学の基礎づけの試みを紹介する。
チューリングマシンと計算の理論
チューリングマシンを学ぼう!

「チューリング・マシン」は、今から80年以上前の1936年に、当時24歳だったアラン・チューリングが計算のモデルとして提案した、とてもシンプルな構造を持つ「マシン」です。
もちろん、その時代には、現在のようなコンピューターは、影も形もありませんでした。それにもかかわらず、チューリング・マシンは、コンピュータの働きの最も重要なモデルであり続けています。それは、驚くべきことです。
2のn乗の話(Turingマシンについて)
今回の「楽しい数学」のトピックは、2のn乗の話です。
なにか簡単な話に見えますが、意外と広がりがあります。
第一話は「2のn乗の意味を考える」です。
第二話は「直線の上に点は何個あるか?」です。
第三話は、「計算できる数は何個あるか?」です。
ここでは、「計算できる数」についての、チューリングの仕事を紹介します。
人工知能と計算科学 — 計算複雑性入門
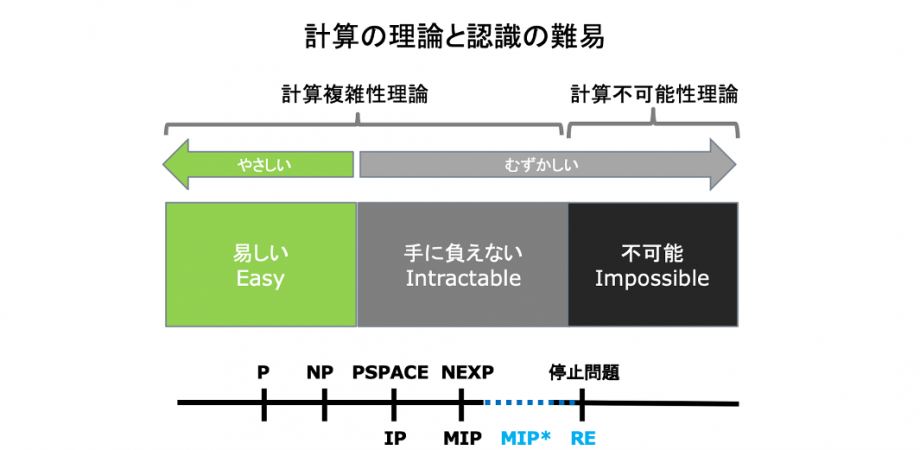
このセミナー「人工知能と計算科学」では、ITの世界の「人工知能」と「計算科学」という二つの領域との関係を通じて、「複雑性理論」での新しい発見が、ITの世界にとって持つ意味を考えてみたいと思います。
チューリングマシンの拡大と複雑性
私たちの認識は単純なものから複雑なものに進みます。世界は複雑なものであふれているので、我々の認識もどんどん複雑になっていきます。ただ、こうした私たちの認識の前進がいつまでも続くとは限りません。私たちの認識は、しばしば、複雑さの前に立ちすくみます。複雑なものを理解するのには、長い時間と膨大な知識の集積が必要であることは、科学の歴史を見れば分かります。
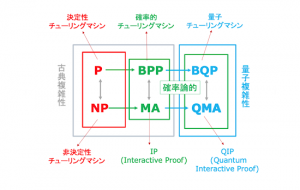
「Interactive Proof 入門」 第三部「確率と証明」
コンピュータ・サイエンスの現在 — MIP*=RE定理とは何か?–
MIP*=RE 入門– Interactive Proofとnonlocal ゲーム —
コンピュータ、数学の問題を解き始める

この2月に、 Open-AI はとても興味深い発表を行いました。彼らは、国際数学オリンピックのいくつかの問題をコンピュータを使って解いて見せたのです。
ただ、今回のセミナーで伝えたいことは、こうした「成果」を、「ニューラル・ネットワーク」や「ディープ・ラーニング」、一般に AI 技術と言われるものの「成果」と単純に見做すべきではないということです。
丸山は、コンピュータ・プログラムが、もともと「論理=数学的推論」を行う能力を持っていると考えています。それは、いわゆるAI技術に基づいて「論理=数学的推論」を実現しようというのとは異なる視点です。
並列・分散アルゴリズム
分散合意アルゴリズム — Paxos

クラウド技術はもちろんネットワーク技術なのですが、クラウド技術成立の前提には、「ネットワーク上で規模を拡大しながら、システム全体としては障害を起こさないシステムを作ることは難しい」という認識があったことです。この認識は「ハードウェアの障害は起きるものだ」という障害観の成立とともに、重要なものだと思います。
Paxosは、いわば、こうした認識の中で生まれた、大規模分散システムの心臓部と言っていいアルゴリズムです。
並列・分散アルゴリズムの基礎

「排他制御 Mutual Exclusion 」「生産者・消費者同期 Producer-Consumer Synchronization 」といった基本的な並列アルゴリズムを学びます。
これらのアルゴリズムは、1960年代の半ばにダイクストラらによって定式化されたもので、計算科学のいわば「古典」と言ってもいいものです。ただ、こうした知識が、現代では不要になったわけではありません。セミナーの骨組みは、2015年のランポートのTuring賞受賞講演に全面的に依拠しています。




