チューリングマシンの拡大と複雑性
「チューリングマシンの拡大と複雑性」概要
私たちの認識は単純なものから複雑なものに進みます。世界は複雑なものであふれているので、我々の認識もどんどん複雑になっていきます。ただ、こうした私たちの認識の前進がいつまでも続くとは限りません。私たちの認識は、しばしば、複雑さの前に立ちすくみます。複雑なものを理解するのには、長い時間と膨大な知識の集積が必要であることは、科学の歴史を見れば分かります。
僕は、対象の複雑さと認識の複雑さは同じものだと考えています。そうした認識は「複雑さ」そのものを対象とした認識が可能だということを意味します。現代の計算科学のもっとも活発な研究分野はの一つは「複雑性理論」なのですが、そうした理論が登場したことの意味は、そう考えれば、よく理解できると思います。
今回のセミナーでは、様々なチューリングマシンの拡大といくつかの基本的な複雑性のクラスの対応を紹介したいと思います。次のようなチューリングマシンを取りあげます。
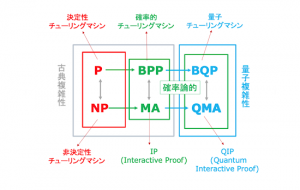
● 決定性チューリングマシン
● 非決定性チューリングマシン
● 確率性チューリングマシン
● 量子チューリングマシン
先に、「複雑なものを理解するのには、長い時間と膨大な知識の集積が必要である」と書きましたが、このチューリングマシンによる複雑さのモデルでは、複雑なものを理解するのに必要な「長い時間」がチューリングマシンの「計算時間」に、「膨大な知識の集積」がチューリングマシンの「テープの長さ」に対応すると思って構いません。
「そんな単純化で大丈夫か?」
確かに。
もちろん、科学の歴史をチューリングマシンに喩えようと思っているわけではありません。ただ、こうした単純化(「抽象化」は、単純化に他なりません)された切り口が、「認識の有限性と対象の無限性」「古典論と量子論」「決定論と確率論」といった認識の大きな問題にアプローチする一つの有効な手段を提供するという話ができればと思っています。
チューリングマシンの拡大と複雑性
全体の概要
↑ 見出しクリックでYouTubeへ; ↓ pdfはスクロールで全文読めます
非決定性チューリングマシンとNPクラス
↑ 見出しクリックでYouTubeへ; ↓ pdfはスクロールで全文読めます
非決定性チューリングマシンと決定性チューリングマシン
↑ 見出しクリックでYouTubeへ; ↓ pdfはスクロールで全文読めます
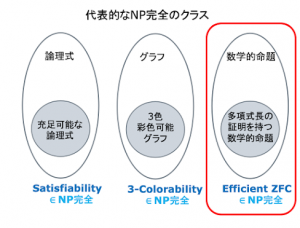
NP完全と数学的証明
↑ 見出しクリックでYouTubeへ; ↓ pdfはスクロールで全文読めます
確率的チューリングマシンとBPPクラス
↑ 見出しクリックでYouTubeへ; ↓ pdfはスクロールで全文読めます
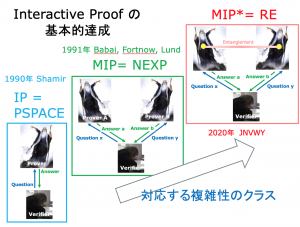
Interactive Proofと証明概念の変化
↑ 見出しクリックでYouTubeへ; ↓ pdfはスクロールで全文読めます
解説
複雑さについて 基本編
複雑さについて (blog)
無限について (blog)
有限の「限界」を考える (blog)
「多項式時間」について (blog)
長い長い計算 (blog)
関数の増大のイメージとBig O記法 (blog)

複雑性の基本的階層
「時間計算量」と「空間計算量」(blog)
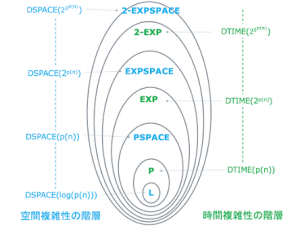
「やさしい問題」と「むずかしい問題」(blog)
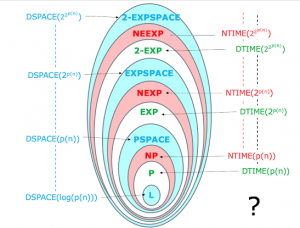
「NP-完全」問題 (blog)
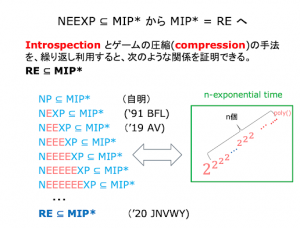
Interactive Proofと MIP*=RE
グラフの3色塗り分け問題 (blog)
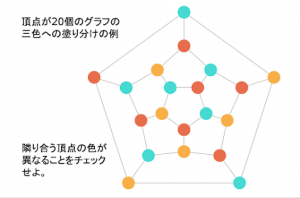
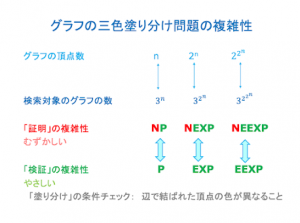
グラフの三色塗り分け問題の複雑性 (blog)
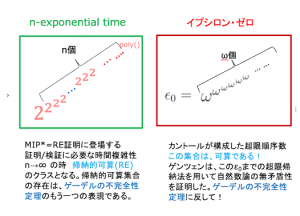
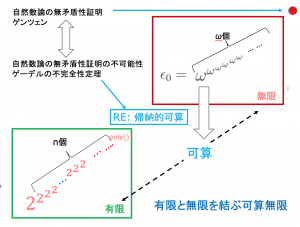
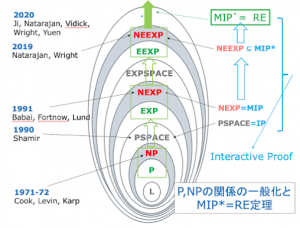
N**Pクラスの階層とMIP*=RE定理 (blog)
有限の中の無限、無限の中の有限 (blog)