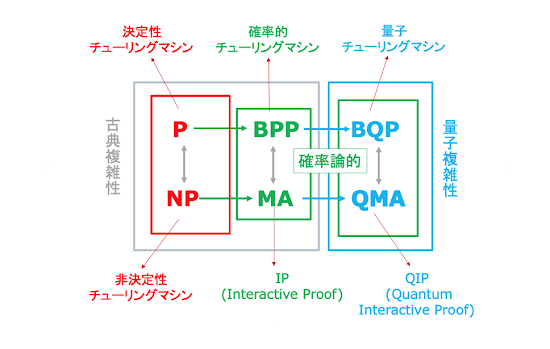
計算科学と計算複雑性
人工知能と計算科学
このセミナー「人工知能と計算科学」では、ITの世界の「人工知能」と「計算科学」という二つの領域との関係を通じて、「複雑性理論」での新しい発見が、ITの世界にとって持つ意味を考えてみたいと思います。
人工知能と複雑性理論
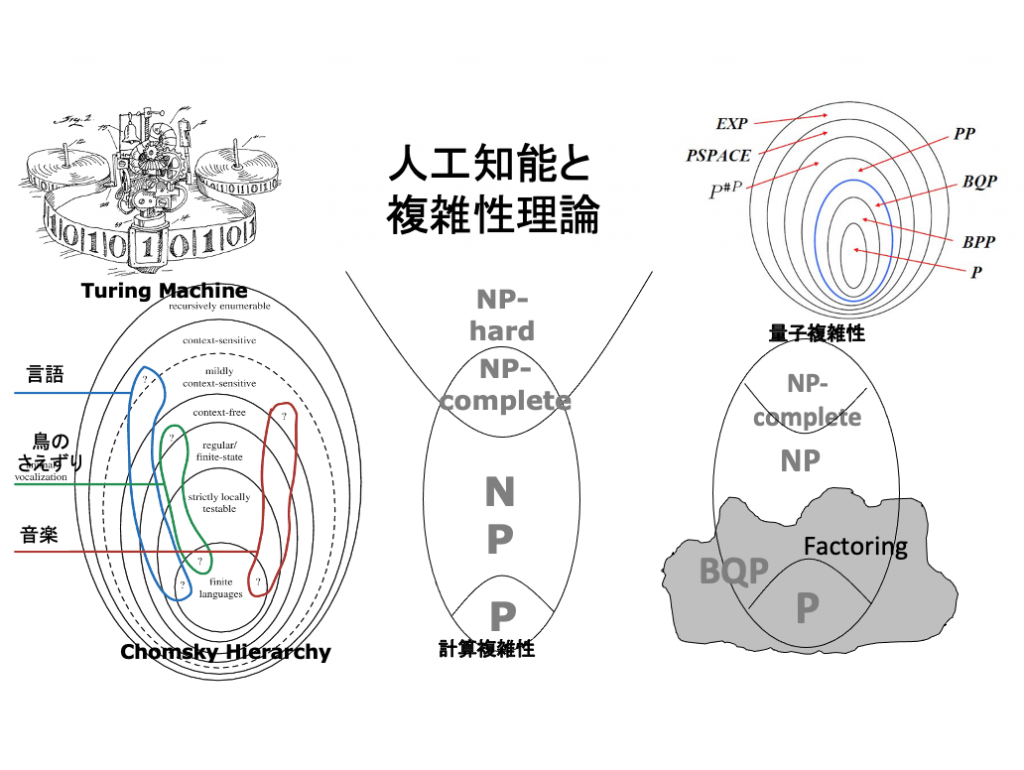
小論は、人口知能研究の今後の発展の方向を、数学的・物理学的認識可能性の理論でもある「複雑性理論」の成立・発展を中軸にして考察したものである。 人間と機械の数学的・物理的認識の限界(筆者は、両者は同じ限界を持つと考えている)を知ることは、すなわち、人工知能の認識の限界を知ることに他ならない
人工知能と量子コンピュータ — NP-完全問題とその含意
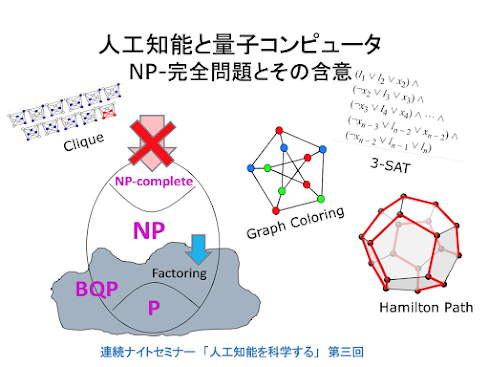
量子コンピュータが、人間の認識の「限界」をどのように拡大するかは、人工知能の未来を考える上で、重要な問題です。 BQP(量子コンピュータで多項式時間で解ける問題のクラス)が、P(古典的コンピュータで多項式時間で解ける問題のクラス)を完全に包含していることの発見と、その応用としてのShorの素因数分解アルゴリズムの発見は、今なお、量子複雑性理論と量子アルゴリズムの金字塔です。
型の理論入門
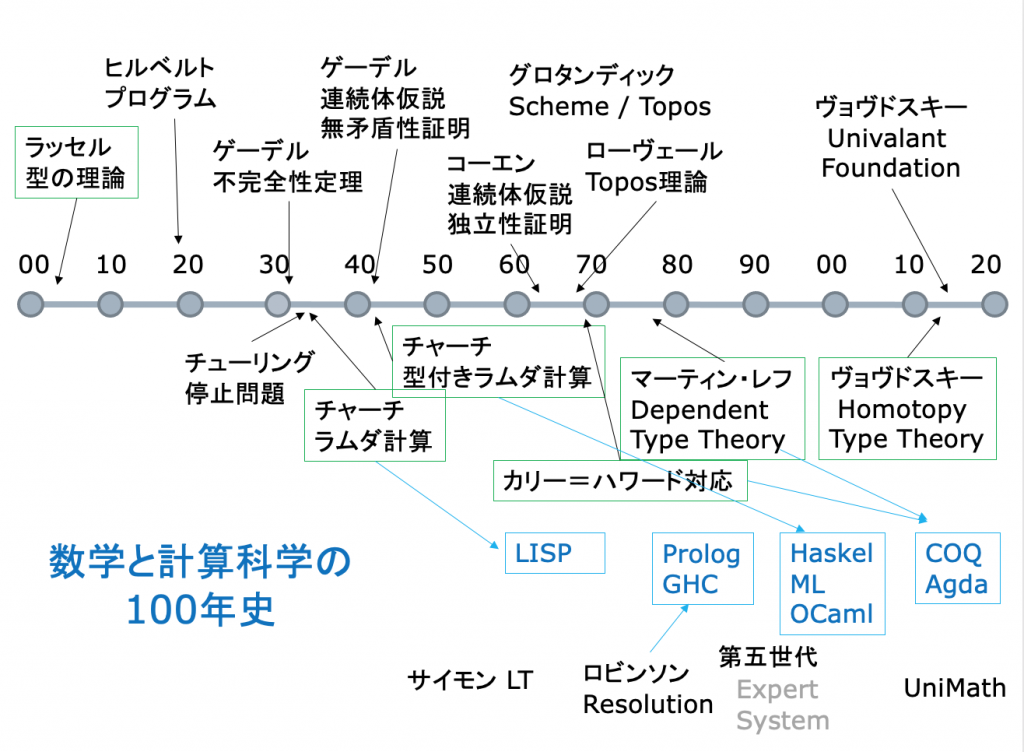
「型があるウログラム言語」と「型のないプログラム言語」があることを、多くのプログラマーは知っていると思います。また、その「どちらがいいか」という「論争」があることも知っていると思います。自分が、日常的にどの言語を使うかは、自分で決めればいいことだと思います。
ただ、「計算」と「プログラム」の本質的な特徴を知るには、「型の理論」が不可欠だと丸山は考えています。
「同じ」を考える — 「型の理論」入門

「同じ」あるいは「同じではない」という判断は、知覚にとっても認識にとっても、最も基本的な判断の一つである。認識の対象が、自然であれ、人間であれ、あるいは、思惟が産み出す抽象的な概念であれ、その認識の土台には、対象の「同一性」についての判断があるように思う。セミナーでは、また、一昨年急逝した数学者のVoevodskyの「同一性」をキーコンセプトにした数学の基礎づけの試みを紹介します。
計算科学と計算複雑性 チュートリアル
チューリングマシンを学ぼう!
「チューリング・マシン」は、今から80年以上前の1936年に、当時24歳だったアラン・チューリングが計算のモデルとして提案した、とてもシンプルな構造を持つ「マシン」です。
もちろん、その時代には、現在のようなコンピューターは、影も形もありませんでした。それにもかかわらず、チューリング・マシンは、コンピュータの働きの最も重要なモデルであり続けています。それは、驚くべきことです。

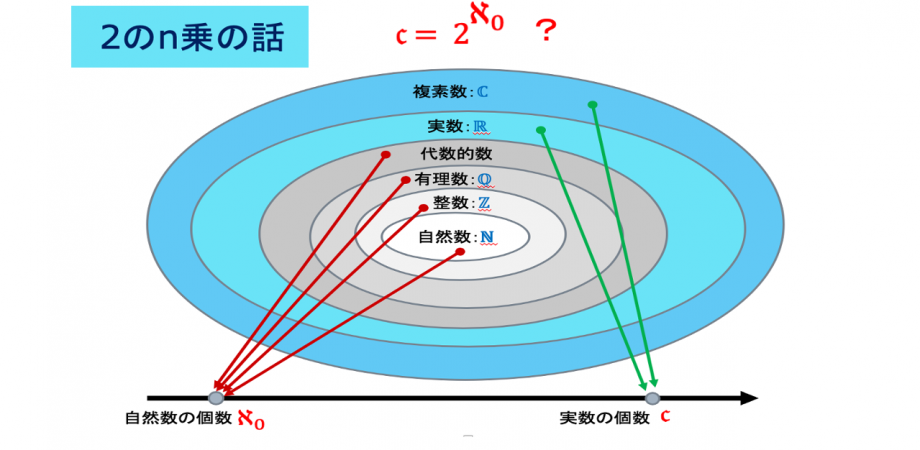
2のn乗の話(チューリングマシンの話)
今回の「楽しい数学」のトピックは、2のn乗の話です。
なにか簡単な話に見えますが、意外と広がりがあります。
第一話は「2のn乗の意味を考える」です。
第二話は「直線の上に点は何個あるか?」です。
第三話は、「計算できる数は何個あるか?」です。
ここでは、「計算できる数」についての、チューリングの仕事を紹介します。
はじめてのCoq
Coqは、現在最も注目されている言語の一つです。
Coqは、「プログラムの正しさの形式的検証手法の再評価」「仕様と実装の関係の見直し」といった形で、ソフトウェア・エンジニアリングの世界に、大きなインパクトを与えようとしています。
「Interactive Proof 入門」に向けて
Interactive Proof 理解のためのblog集です。次のようなタイトルを持つ4つのblog群からなります。
人は、正しくないことを信ずることがあること
神託、魔法使い、数学的証明
複雑性理論と人工知能 複雑さについて

機械と人間のインタラクション
Coq スタートアップセミナー (平原ゼミ)
これからCoqを学習したい人を対象にい、すぐにCoqを使用できるように
Coqの実行環境の紹介し、Coqの実行環境のインストール方法を説明します

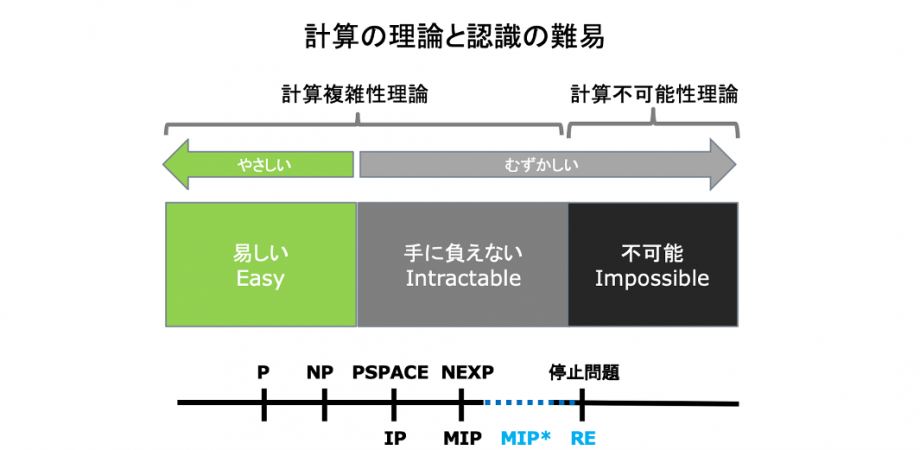
計算科学と計算複雑性 Advanced
チューリングマシンの拡大と複雑性
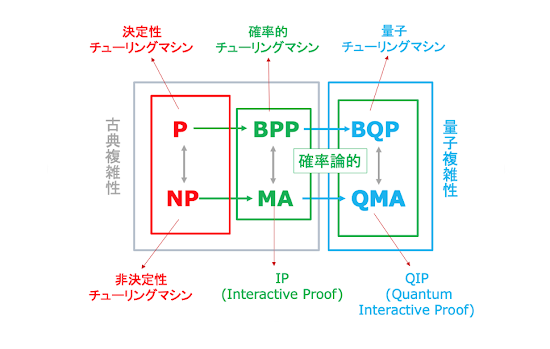
私たちの認識は単純なものから複雑なものに進みます。世界は複雑なものであふれているので、我々の認識もどんどん複雑になっていきます。ただ、こうした私たちの認識の前進がいつまでも続くとは限りません。私たちの認識は、しばしば、複雑さの前に立ちすくみます。複雑なものを理解するのには、長い時間と膨大な知識の集積が必要であることは、科学の歴史を見れば分かります。
コンピュータ・サイエンスの現在 — MIP*=RE定理とは何か?–
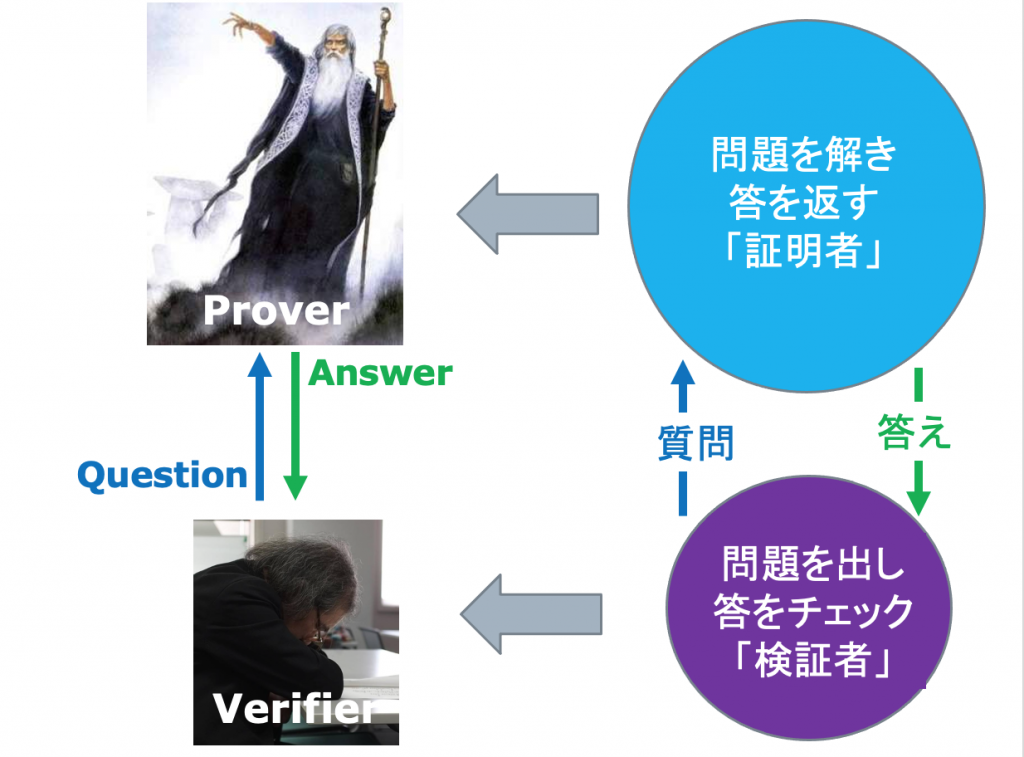
コンピュータ・サイエンスは、今、大きな転換点を迎えています。
その変化は、一言で言えば、コンピュータ・サイエンスは、単に「コンピュータ=計算機についての理論」ではなく、情報理論や物理学や数学などの数学的手法を用いる幅広い数理科学の中心的な理論として登場しつつあると言うことです。
こうしたコンピュータ・サイエンスの進化を象徴的に示すのが、2020年の1月に証明された “MIP* = RE定理”(「ミップ・スター・イコール・アールイー定理」と読みます)です。
MIP*=RE 入門– Interactive Proofとnonlocal ゲーム —

このセミナーでは、MIP* = RE 定理を、interactive proof と nonlocal ゲームの基礎から解説します。セミナーでは、「MIP* = RE」定理の証明の骨組みを構成している、「停止問題」から、二人のプレーヤーによるnonlocalゲームがエンタングルした値1を持つかあるいは最大でも1/2の値を持つかどちらかなのかを決定する問題への、実効的な還元が存在するというロジックの大まかな流れを紹介しようと思います。
計算科学とエントロピー — コロモゴロフ複雑性とアルゴリズム論的情報理論

今回のマルゼミ「計算科学とエントロピー — コロモゴロフ複雑性とアルゴリズム論的情報理論」では、ボルツマンやシャノンとは異なるエントロピーへのアプローチを取り上げます。「アルゴリズム論的情報理論 (“Algorithmic information theory”)」といわれるものです。
「アルゴリズム論的情報理論」は、計算科学でのチューリング=チャーチらの計算可能性の理論と、シャノンの情報理論とを結びつけようという試みです。
Interactive Proof 入門
nonlocal game とInteractive Proof
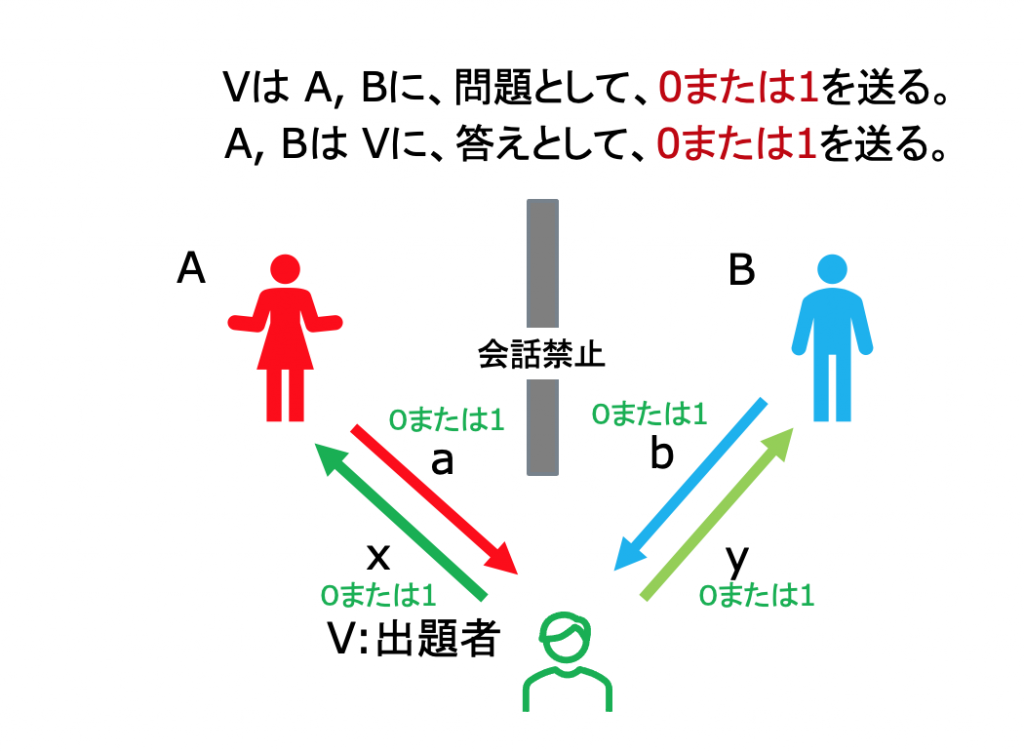
Bellの洞察をゲーム形式に翻案したCHSHゲームについて学びます。プレーヤー二人がエンタングルした情報を共有する non-local ゲームの「勝率」を計算することを通じて、古典論とは異なる量子論的相関の実在性を示すことができます。CHSHゲームの形式は、Interactive Proof の形式と同じものです。
確率と証明

確率的推論と数学的演繹は、別々の認識のスタイルに属すると長いこと考えられてきました。ただ、近年の数学的認識の発展は、両者の間の驚くべき繋がりを明らかにしてきました。
それは、広い意味では、決定論的ではない確率論的な量子論的認識の広がりに対応するものだとぼくは考えています。
この分野では、女性の活躍が目立ちます。
Interactive Proofと複雑性
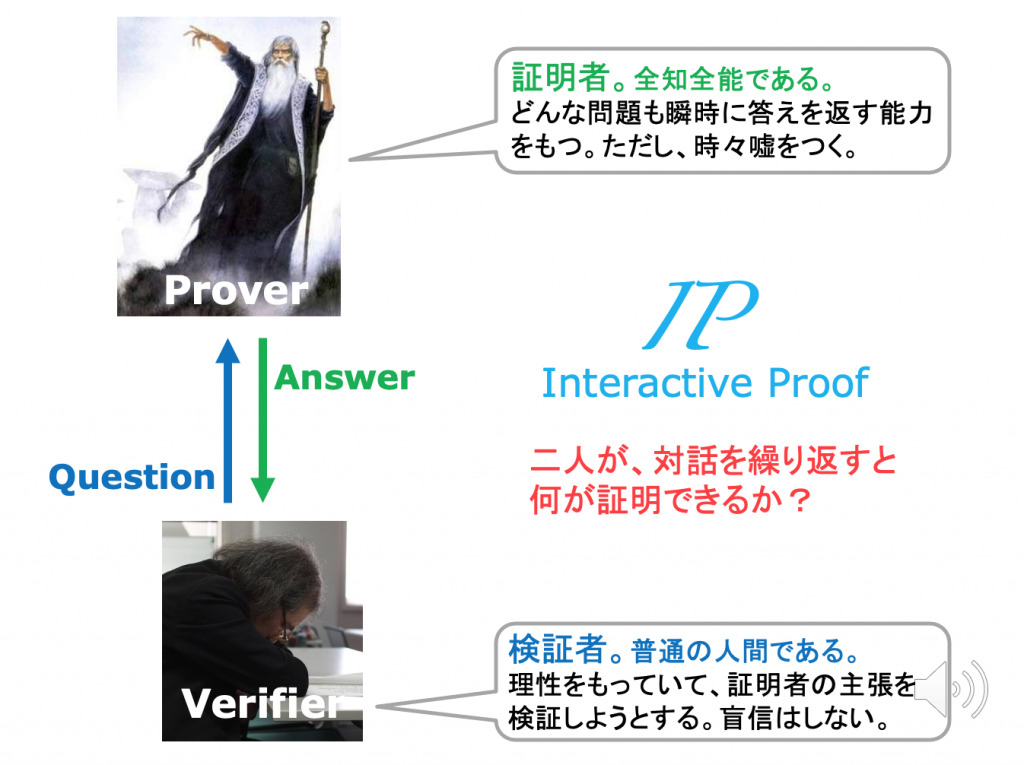
新しい複雑性のクラスの特徴付けに、大きな役割を果たしたのは、Interactive Proof の手法でした。ここでは、グラフの同型性の複雑さの認識を例に、をその代表的な事例を振り返ります。