2のn乗の話(Turingマシンについて)
セミナー概要
今回の「楽しい数学」のトピックは、2のn乗の話です。
なにか簡単な話に見えますが、意外と広がりがあります。お楽しみに。
いずれの話も、特別の数学的な前提知識は必要ではありません。皆さんのおこしをお待ちしています。
第一話は「2のn乗の意味を考える」です。
● IT の世界の人は、1, 2, 4, 8, 16, 32, 64, … という2のn乗の並びはよく知っていますね。2の10乗が1024で、1K Byteの単位になっていることも。
● 2のn乗は、また、二つのものを重複を許してn個並べる順列の数です。それは、二進数でn桁の0と1の並びの数を考えればわかります。
● 2のn乗は、n個の要素を持つ集合の、部分集合の数です。
● 2のn乗は、定義域が n = { 0, 1, 2, … , n-1} で値域が 2 = {0, 1} に値を取る全ての関数の数を表します。
● …
第二話は「直線の上に点は何個あるか?」です。
第一話との関係が、すぐにはわかりにくいかもしれません。でも、関連があるんです。
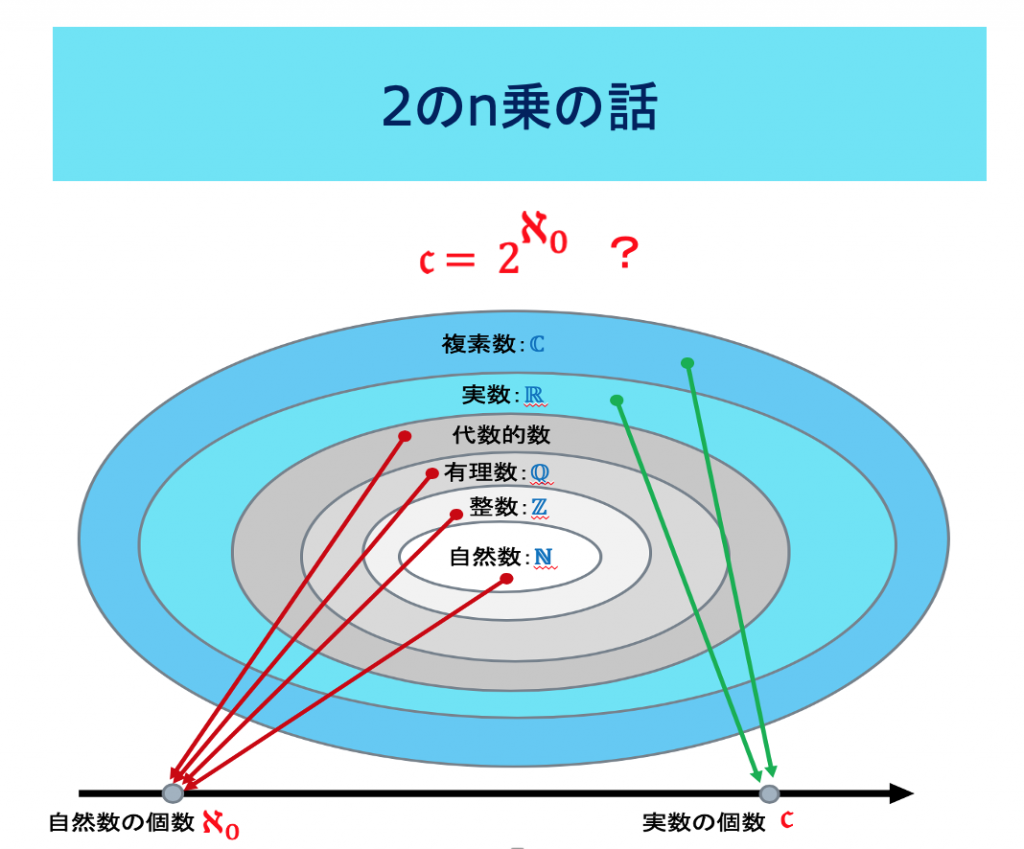
集合論の創始者のカントールは、自然数の個数をn とすれば、実数の個数は 2のn乗になることを予想しました。これを「連続体仮説」と言います。残念ながら、カントールは、このことを証明できませんでした。
第三話は、チューリングマシンについて基本的なことを確認しています。それは第四話の準備になっています。チューリングマシンについてはマルレク「チューリングマシンを学ぼう!」の「チューリングマシンの基礎」を参照ください。
第四話は、「計算できる数は何個あるか?」です。
ここでは、「計算できる数」についての、チューリングの仕事を紹介します。
彼は「計算する機械」(彼の名前をとって「チューリング・マシン」といいます)を具体的に構成して、「定義はできるけど、実際に計算できない数がある」ことを示しました。内容的には、有名なゲーデルの「不完全性定理」と同じようなものです。不完全性定理、難解だと思っている人が多いのですが、それらの不思議な主張は、第二話で述べた、自然数の個数と実数の個数の大きな「違い」に注目すれば、直観的に理解することができます。
(2020/06/30 楽しい数学)
セミナー解説資料
「2のn乗」の様々な解釈
「2のn乗は関数を表す」という話
↑ 見出しクリックでYouTubeへ; ↓ pdfはスクロールで全文読めます
「一対一対応」の話
↑ 見出しクリックでYouTubeへ; ↓ pdfはスクロールで全文読めます
「実数の個数は自然数の個数より多い!」
↑ 見出しクリックでYouTubeへ; ↓ pdfはスクロールで全文読めます


