
認識について
認識について考える

今回のマルレクは、人間の認識について考えます。
まず、認識を情報の言葉で語ってみようと思います。認識論には、西洋哲学ではプラトン、アリストテレス以来の長い歴史があるのですが、伝統的な哲学的認識論には「情報」という概念はありません。「情報」という概念は、新しいものです。現代の我々の認識は、新しい情報の世界と深く結びついています。情報の時代、人間の認識は、そのスタイルにおいてもその能力においても、大きく変わりつつあります。
認識について考える 2 — 認識の認識

今回のマルゼミは、前回のマルレク「認識について考える」の続編です。前回は、主要に、自然認識とそれを可能とする条件の変化の歴史を振り返ったのですが、今回は、「認識の認識」という構造に注目しようと思います。認識の対象となるのは、自然ではなく、認識そのものです。
具体的な自然認識を対象とした前回からは、少し飛躍があるのですが、今回のセミナーでは、「認識の認識」を、「認識の形式的・数学的認識」として捉えるというアプローチを取ってみようと思います。認識のいくつかの特徴を、形式的・数学的に把握することが可能であるという立場をとります。
情報とエントロピー

確率的な分布は、いろんなところに現れます。重要なことは、どんなところに現れる確率分布にも、我々はエントロピーという共通の構造を見出すことができるということです。その意味で、エントロピーは、「物質=エネルギー」とならんで、もっとも基本的な概念の一つです。
人工知能と複雑性理論
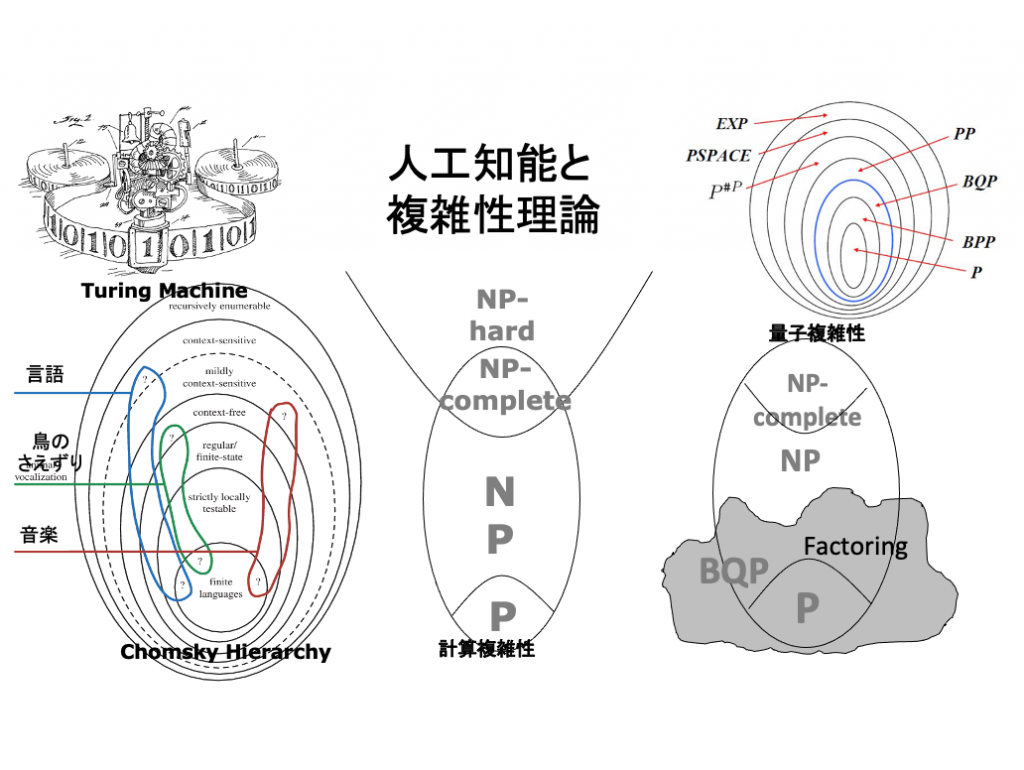
小論は、人口知能研究の今後の発展の方向を、数学的・物理学的認識可能性の理論でもある「複雑性理論」の成立・発展を中軸にして考察したものである。 なぜ、数学的・物理学的認識が問題になるのか?人間と機械の数学的・物理的認識の限界(筆者は、両者は同じ限界を持つと考えている)を知ることは、すなわち、人工知能の認識の限界を知ることに他ならない
自然の認識
たとえ話で理解する量子の世界

「量子の世界」を知るのに数学を利用するための準備を、数学を使わないで行います。数学の代わりに、ここでは多くの「たとえ話」を使おうと思います。
エンタングルメントで理解する量子の世界

エンタングルメントは、現代では、量子の世界のもっとも基本的な現象だと考えられています。ただ、エンタングルメントをなにか神秘的で奇妙なものだという印象を持っている人も多いと思います。そういうイメージを払拭したいと僕は考えています。また、それは可能だと考えています。今回のセミナーの目的は、エンタングルメントを、できるだけ多くの人に理解してもらうことです。
ケット |k> で理解する量子の世界

ここでは、量子論を理解するのに必要な数学 — 線形代数の話を、ケット記法を使ってしようと思います。ケット記法は、量子論の最も標準的で基本的なツールです。ケット記法を理解することが、量子の世界を数学的に理解する第一歩になります。
密度行列 ρ で理解する量子の世界

量子の世界を記述するには、ベクトルを使うやり方と密度行列を使うやり方があります。二つのアプローチは、量子の世界を記述しようという点では、基本的には同じ能力を持ちます。このセミナーでは、密度行列を使うやり方を学びます。
エンタングルする自然

このセミナーでは、21世紀の自然観の中核に「エンタングルする自然」という自然観が生まれていることを、「量子論」と「相対論」の対立と統一の歴史を背景に解説します。
エンタングルする認識

今回のセミナー「エンタングルする認識」は、エンタングルメントの認識が、現時点での人間の認識能力の飛躍の中心舞台だという観点から、エンタングルする自然」という自然観を、我々がどのように形成・獲得してきたかをみようとしたものです。
ペンローズの宇宙論

小論は、2020年のノーベル物理学賞を受賞したロジャー・ペンローズの宇宙論の分かりやすい紹介を目指したものです。基本的には、彼の2010年の著作 “Cycles of Time” に依拠しています。ノーベル賞受賞の記念講演で、彼は、主要にこの宇宙論について語っています。
数学的認識
数理哲学への招待
社会が複雑になり、我々の社会的活動が多様になり、また、我々の認識の対象が量子の世界から宇宙まで拡大するにつれ、我々と数学との接点は、ますます広がっていきます。
今度のセミナーの目標は、数学が面白いことを感じてもらうというものにしようと思っています。
楽しい数学 — 好奇心から広がる数理の世界
集合論入門

集合論は、19世紀後半に、ドイツの数学者ゲオルグ・カントールが創り出した数学の一分野です。
集合論の登場は、現代数学の一つの特徴である「抽象化」の歴史的な第一歩といっていいと思います。
集合論は、主要に、無限と連続というものを数学的に考える数学として出発します。ただ、その前途は、平坦なものではありませんでした。
2のn乗の話(チューリングマシンの話)
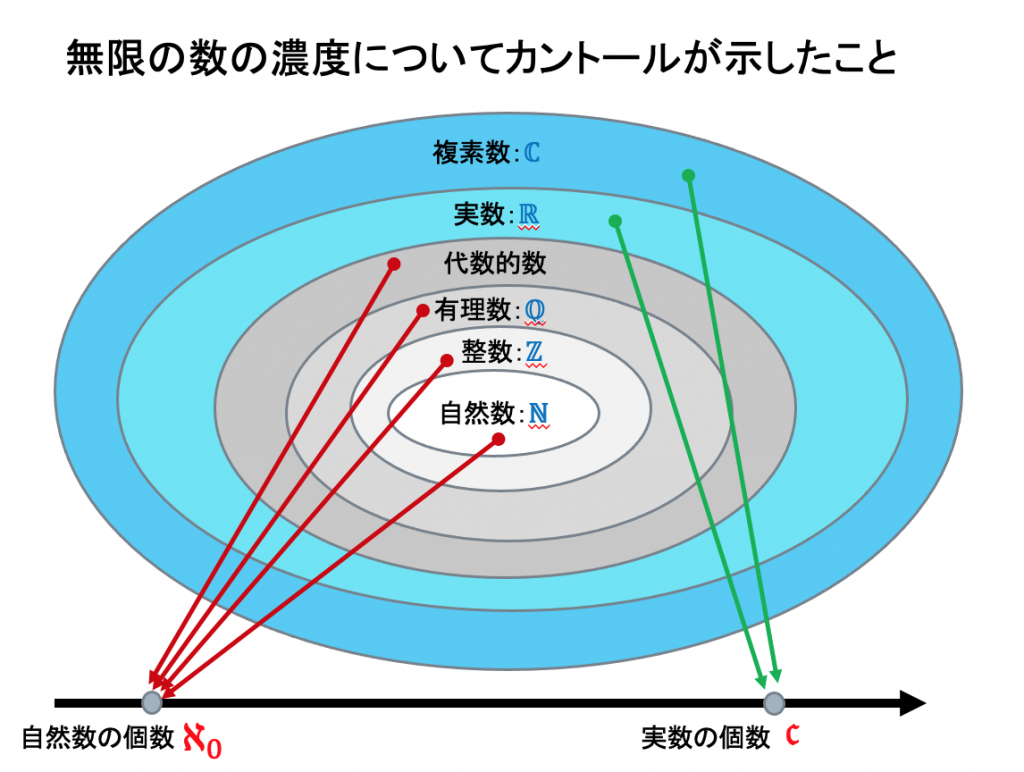
今回の「楽しい数学」のトピックは、2のn乗の話です。
なにか簡単な話に見えますが、意外と広がりがあります。
第一話は「2のn乗の意味を考える」です。
第二話は「直線の上に点は何個あるか?」です。
第三話は、「計算できる数は何個あるか?」です。
ここでは、「計算できる数」についての、チューリングの仕事を紹介します。
数学的認識について / 数学の基礎と計算科学
「型の理論」入門
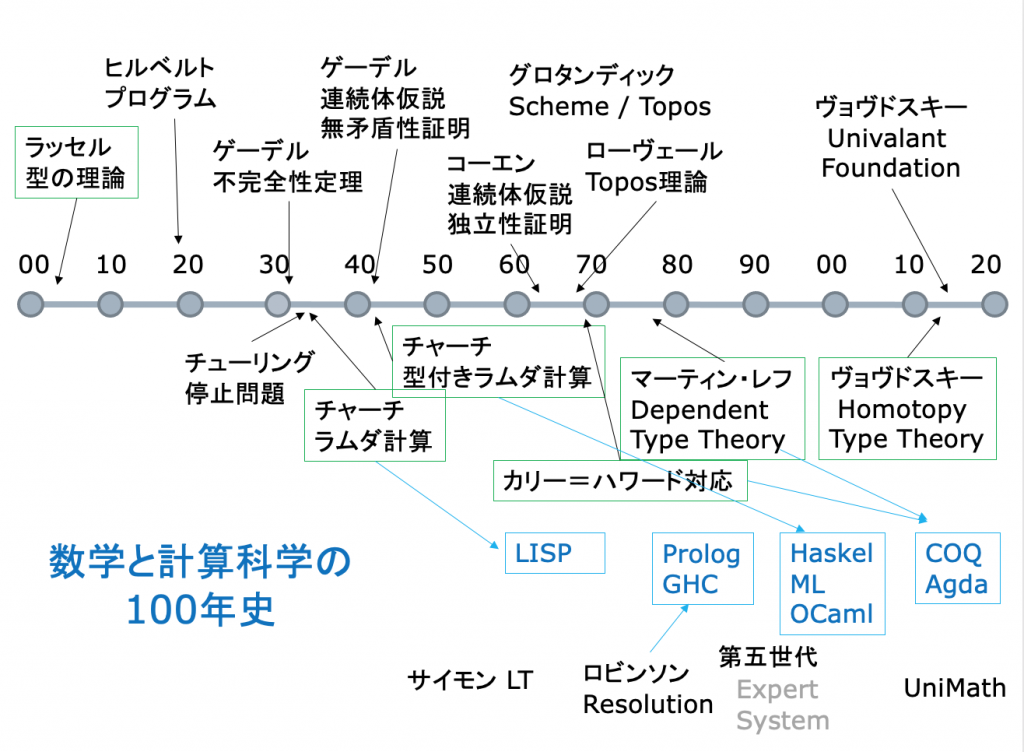
「型の理論」は歴史的には、数学をどのように基礎づけるかという問題と結びついて発展してきました。同時に「型の理論」は、現代では、数学の基礎に対する関心とは、いわば正反対の、数学の実際的応用である計算機科学と密接に結びついています。
「型の理論」が明らかにした、「証明」=「計算」=「プログラム」という三位一体の関係の認識は、21世紀の計算科学の出発点になるべきものだと、僕は考えています。
「同じ」を考える — 「型の理論」入門

「同じ」あるいは「同じではない」という判断は、知覚にとっても認識にとっても、最も基本的な判断の一つである。認識の対象が、自然であれ、人間であれ、あるいは、思惟が産み出す抽象的な概念であれ、その認識の土台には、対象の「同一性」についての判断があるように思う。セミナーでは、また、一昨年急逝した数学者のVoevodskyの「同一性」をキーコンセプトにした数学の基礎づけの試みを紹介します。
チューリングマシンの拡大と複雑性
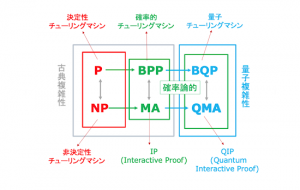
私たちの認識は単純なものから複雑なものに進みます。世界は複雑なものであふれているので、我々の認識もどんどん複雑になっていきます。ただ、こうした私たちの認識の前進がいつまでも続くとは限りません。私たちの認識は、しばしば、複雑さの前に立ちすくみます。複雑なものを理解するのには、長い時間と膨大な知識の集積が必要であることは、科学の歴史を見れば分かります。
コンピュータ・サイエンスの現在 — MIP*=RE定理とは何か?–

コンピュータ・サイエンスは、今、大きな転換点を迎えています。
その変化は、一言で言えば、コンピュータ・サイエンスは、単に「コンピュータ=計算機についての理論」ではなく、情報理論や物理学や数学などの数学的手法を用いる幅広い数理科学の中心的な理論として登場しつつあると言うことです。こうしたコンピュータ・サイエンスの進化を象徴的に示すのが、2020年の1月に証明された “MIP* = RE定理”(「ミップ・スター・イコール・アールイー定理」と読みます)です。