型の理論入門 （ 論理学入門 III ）

型の理論入門　概要

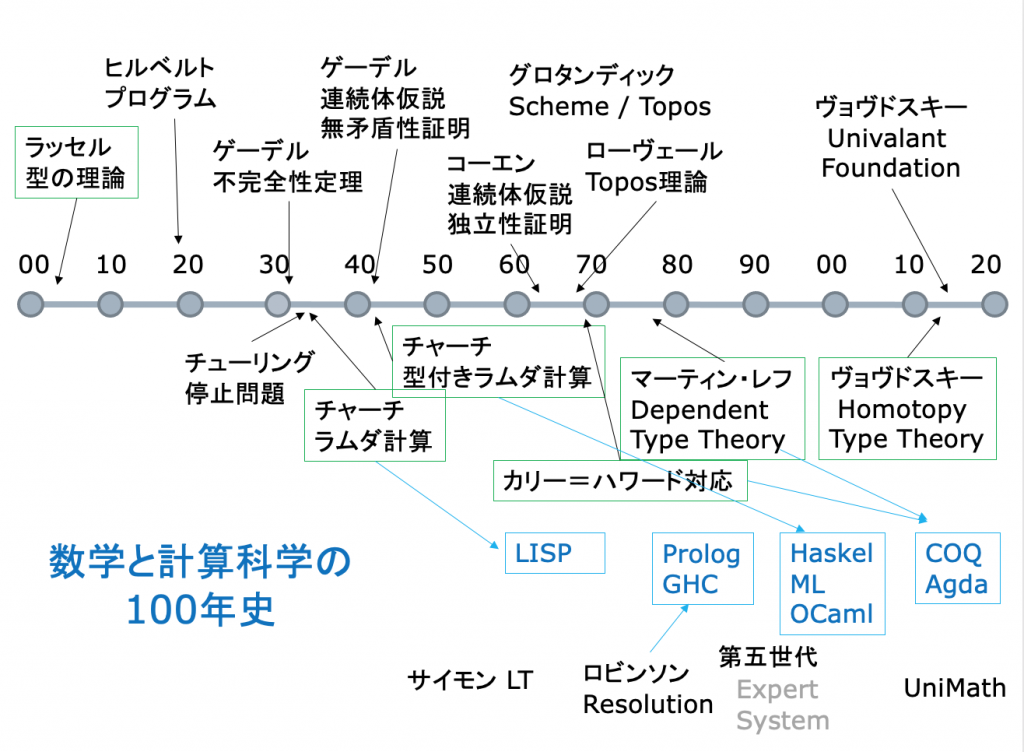
「型の理論」には、Russellの 'Ramified Type Theory' から Voevodsky の 'Homotopy Type Theory' までを数えれば、100年以上の歴史があります。

「型の理論」の歴史には、ひとつ大きな特徴があります。

ラッセルの理論が、自ら発見した「集合論の逆理」がもたらした数学の基礎の「危機」を解消しようとする試みとして生まれたことが示すように、「型の理論」は数学をどのように基礎づけるかという問題と結びついて発展してきました。

Churchのラムダ計算もTuringのTuring machineの構成も、ゲーデルの不完全性定理がもたらした数学の基礎についての「危機」に対する反省・探究の中で生まれたものです。数学の基礎への関心は、集合論、Topos理論にかわる数学の新しい基礎づけを目指したVeovodskyの"Univalent Foundation" まで、一貫して流れ続けています。

「型の理論」には、もう一つの際立った特徴があります。

それは、先に見た数学の基礎に対する関心とは、いわば正反対の、数学の実際的応用と密接に結びついているという特徴です。

60年代以降、現実世界で急速に拡大するコンピュータの利用の拡大に伴って登場した「計算機科学」の基礎として、以前のチャーチやチューリングの「計算」に対する理論的モデルに関心が高まります。そしてそれらの汎用な計算モデルが、汎用の「プログラム言語」としてコンピュータ上で実装されるようになります。McCarthy のLISPは、Churchの「型なしラムダ計算」の実装に他なりません。

こうした数学・論理学の世界での発見が計算科学の世界の新しいプログラム言語の創設にインスピレーションを与えるという関係は今も続いています。

ただ、それにもかかわらず、残念ながら、二つの世界の関係はあまり密なものではありません。

一つの問題は、これ迄の経験から言えば、数学・論理学の世界での発見が、コンピュータの世界で応用されるまでに30年から40年かかるという、とてもとても長いタイムラグがあるということです。

もう一つの問題は、こうしたタイムラグを背景として、二つの世界の住人があまり接点を持たず、お互いに関心をもたないことがあると思います。コンピュータの世界の「遅れ」だけではありません。Voevodskyは、コンピュータ実習室での学生のプログラミングを見て、「従属型の理論」を「再発見」したと正直に語っています。

語りたいことは多いのですが、いずれにせよ、「型の理論」の歴史が明らかにした、「証明」＝「計算」＝「プログラム」という三位一体の関係の認識は、21世紀の計算科学の出発点になるべきものだと、僕は考えています。

多くの人が、「型の理論」に興味を持つことを望んでいます。