論理学入門 I — 命題論理の演繹ルール

2020/01/28 マルゼミ「論理学入門 I」概要
なぜ今「論理学」を学ぶのか?
その理由は、人工知能技術の未来に関係しています。
丸山は、人工知能技術の次の飛躍は、コンピュータの論理的に推論する能力が、現実の課題に広く応用される時に始まると考えています。すでに、そうした動きは始まっています。ソフトウェア・エンジニアリングの分野での「形式手法」への関心の高まりは、その一つの現れです。
「知能」の中核としての「推論する能力」
我々人間の「知能」の中核には、論理的に推論する能力があります。我々は、意識的に、ある場合は無意識のうちに、その能力を日常的に利用しています。例えば、プログラマが与えられた仕様をプログラムとして実装しようとする時、また、プログラムのバグを修正しようとする時、我々は、論理的に考えています。
ただ、その「論理的推論」が、どのように行われているかについて、我々は、必ずしも、自覚的ではありません。それは、日本語を自由に正確に話せるとしても、その発話が日本語の文法に基づいていることを正確に説明できるとは限らないのと同じです。
「推論する能力」を意識的に捉える
重要なことは、機械に論理的推論をさせるためには、我々が行う論理的推論が、どのようなルールに基づいているのかを意識的に捉える必要があるということです。多くのプログラマは、プログラムの条件式の扱いを通じて論理式がどのような真偽の値をとるかについては、よく知っています。残念ながら、論理的推論のルールを知るためには、それだけでは十分ではありません。論理学を学ぶことで、はじめて、その論理的推論のルールを学ぶことができます。
Coqの理解のために
論理学を学ぶことで、一見すると,とっつきにくい Coqの理解は大きく進みます。
Coqを学ぼうとしている人に、このセミナーの受講をお勧めします。
資料の構成
Part I 論理式と推論ルール
単純な論理式とその値
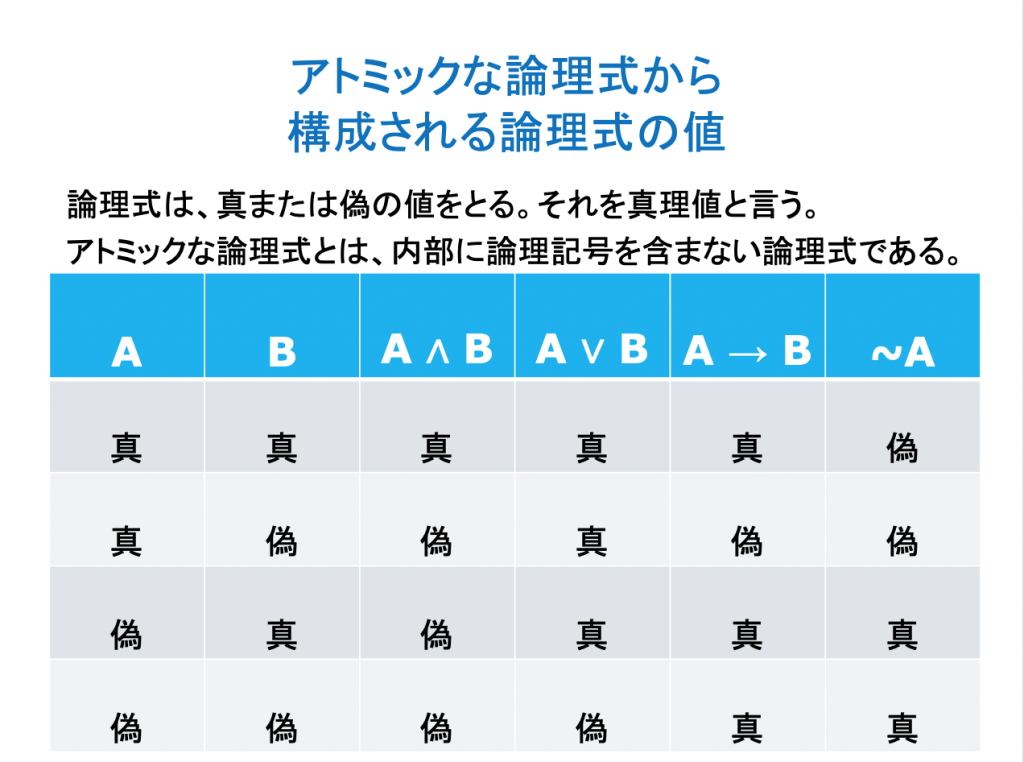
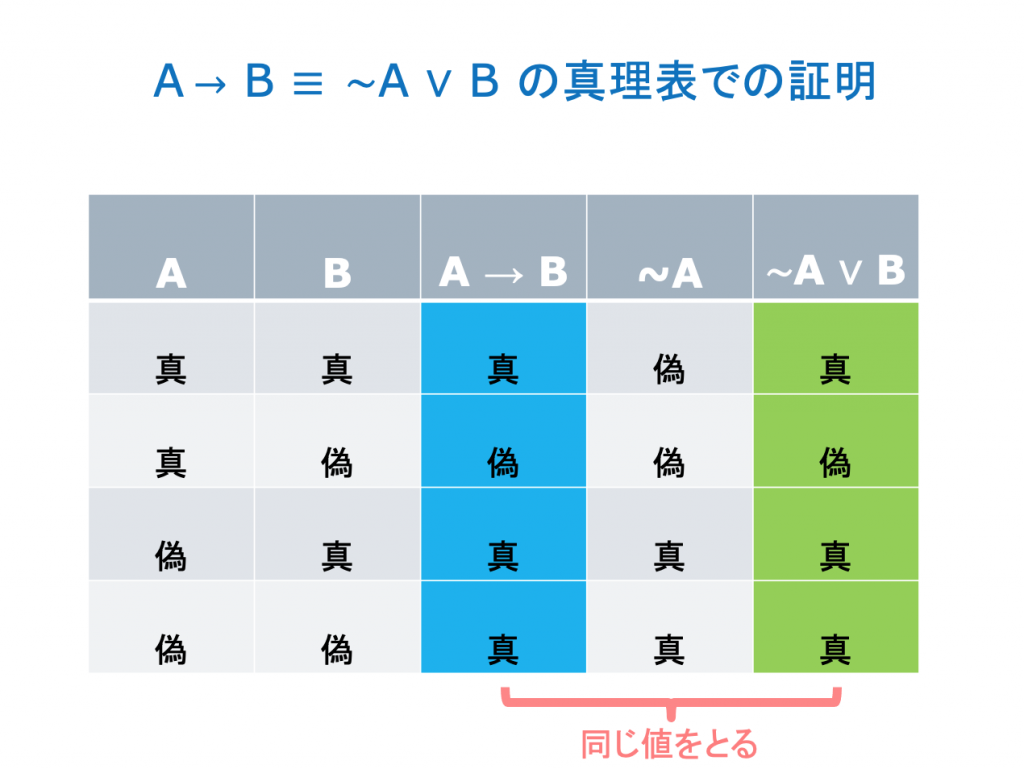
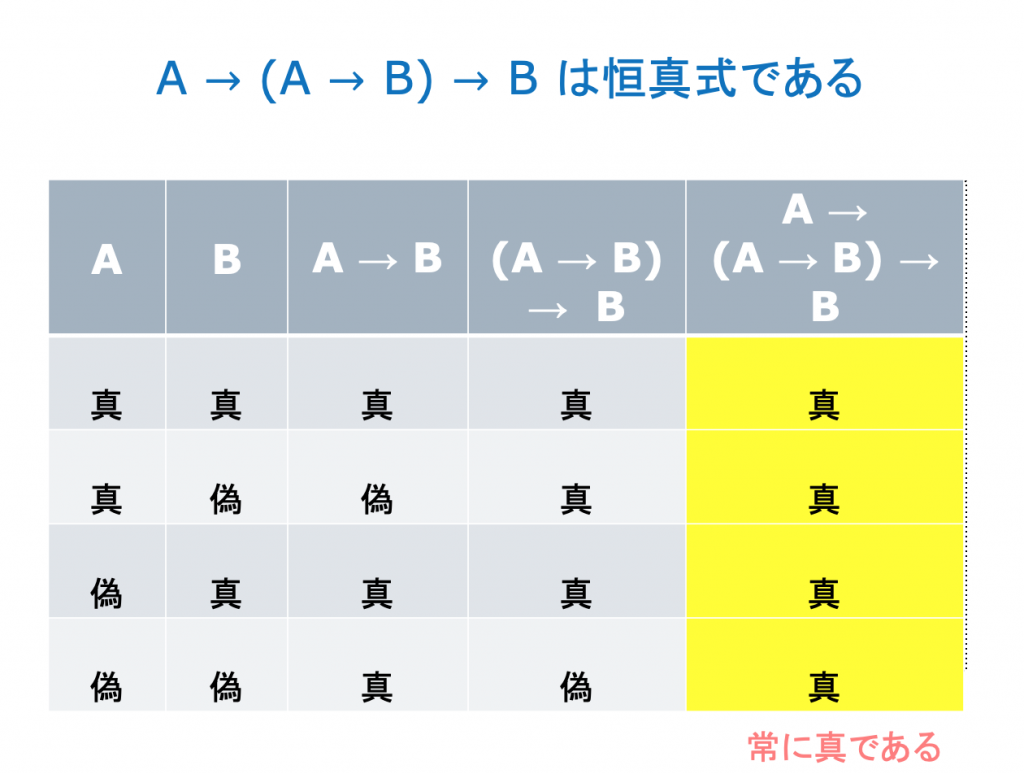
論理式の意味と「判断」について

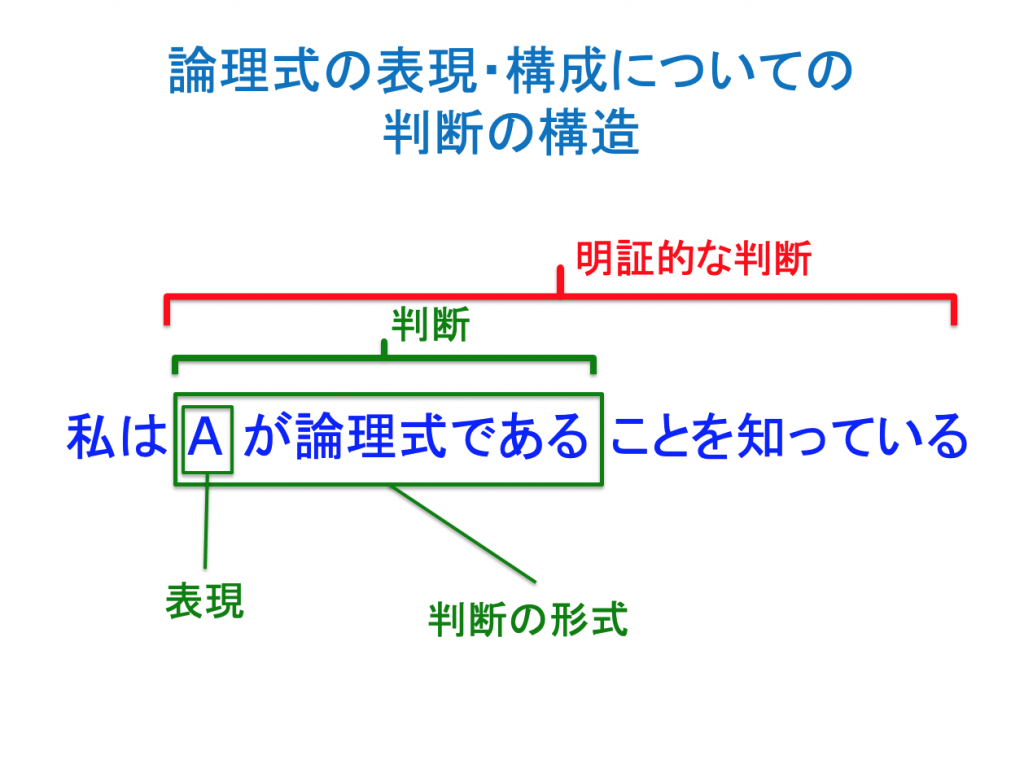
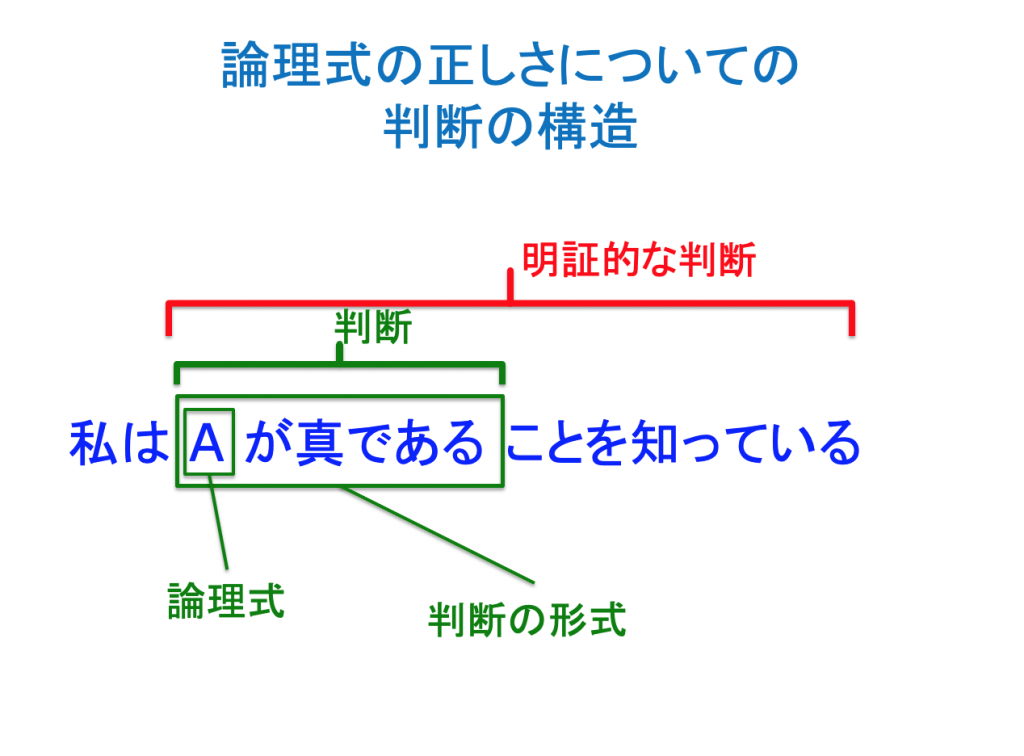
論理式はどのような形をしているか?

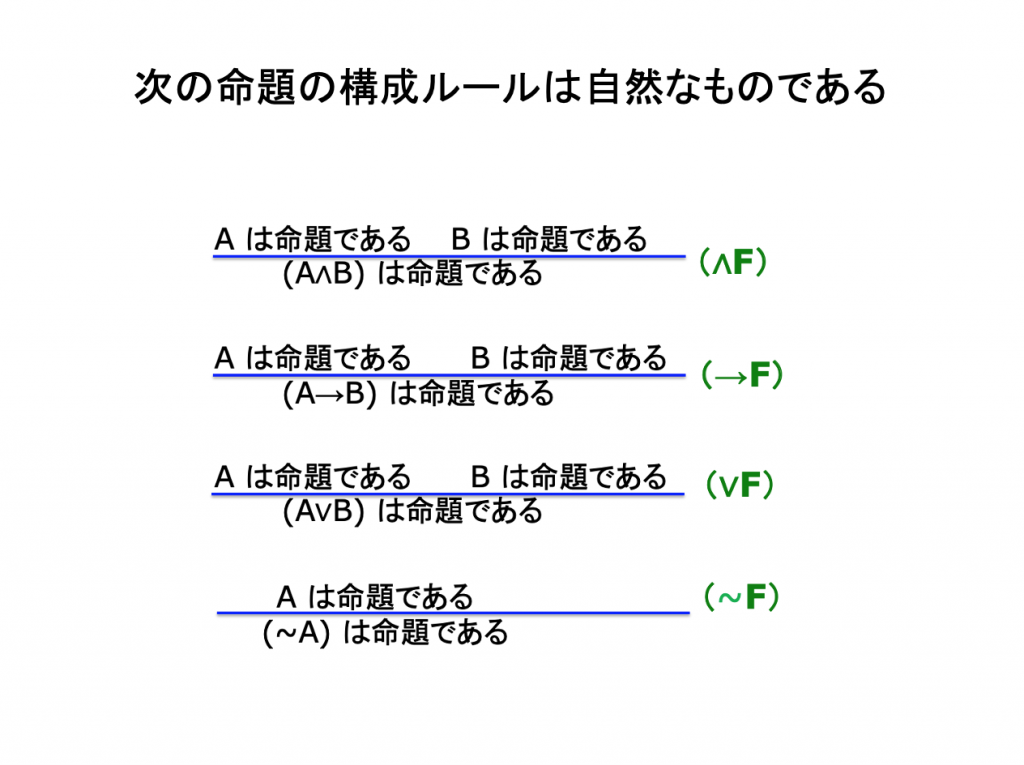
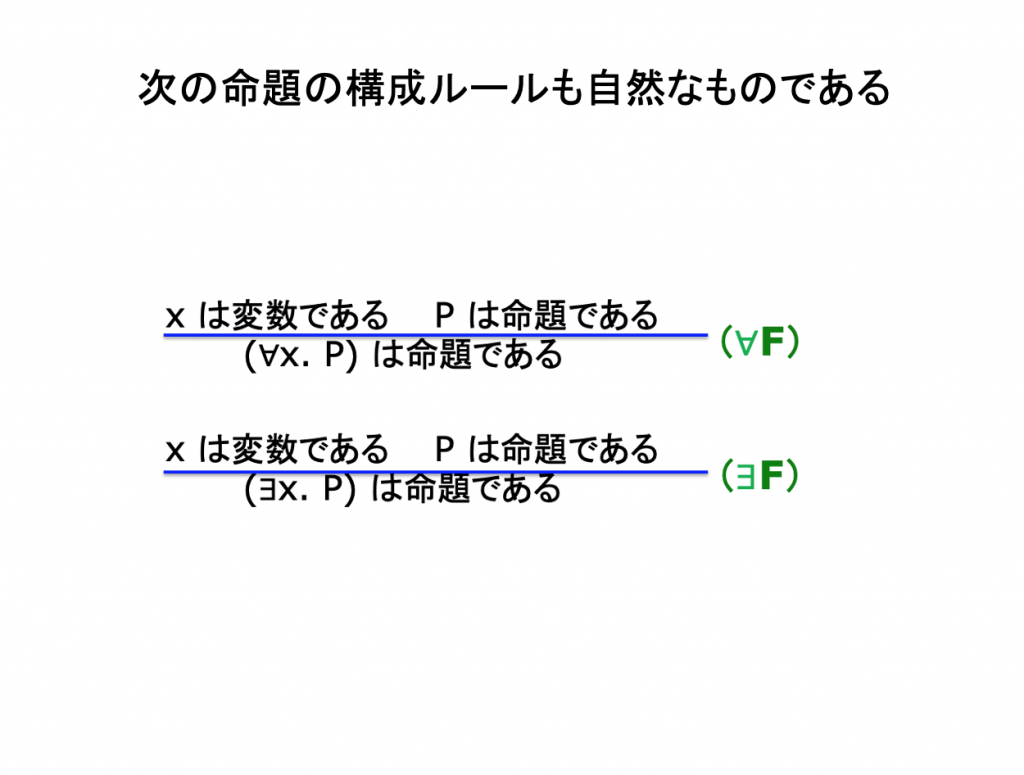
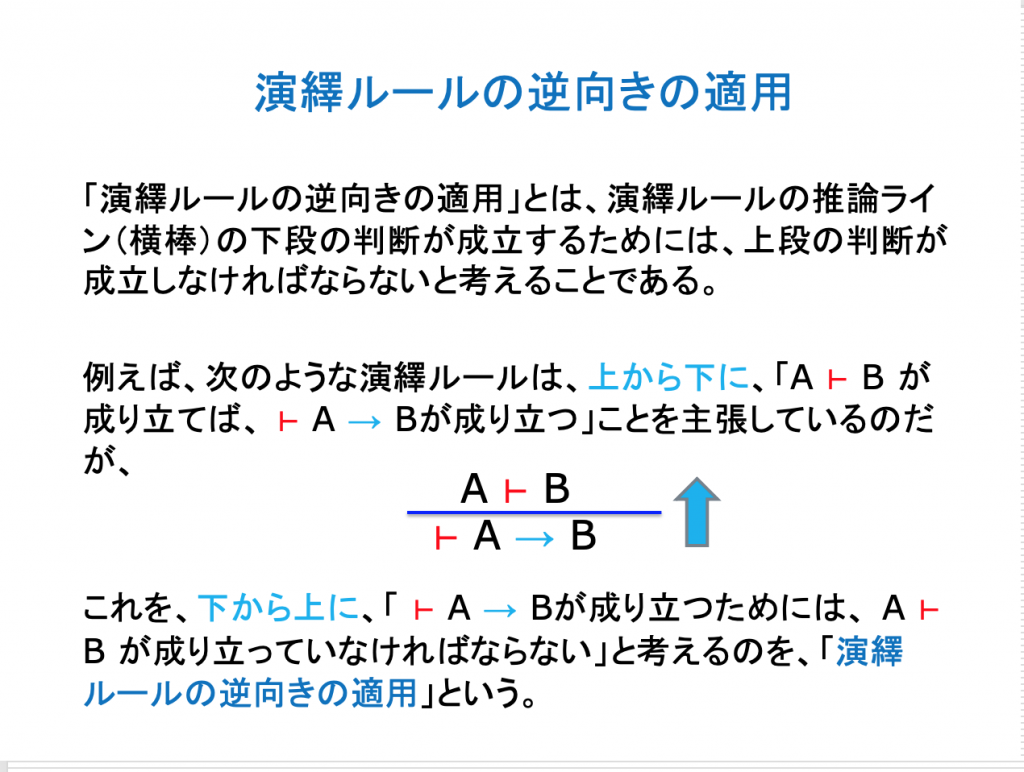
A ⊢ Bという論理的帰結の判断と判断から判断への推論ルール



Part II Sequent Calculus
Sequent Calculusと「証明」


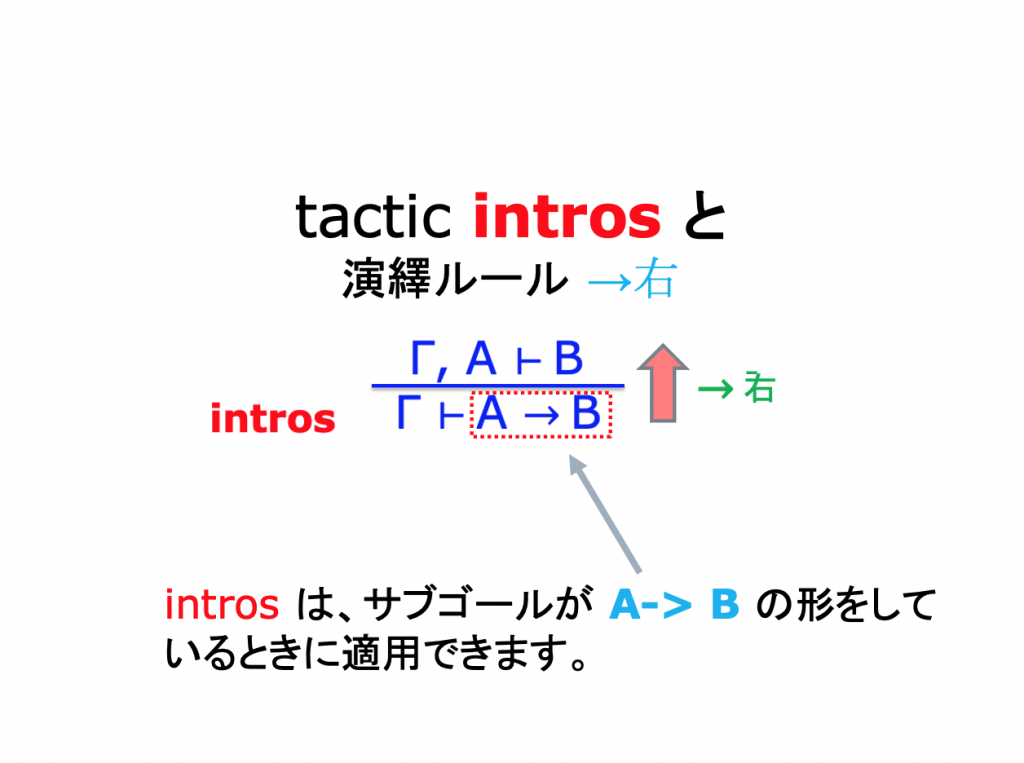
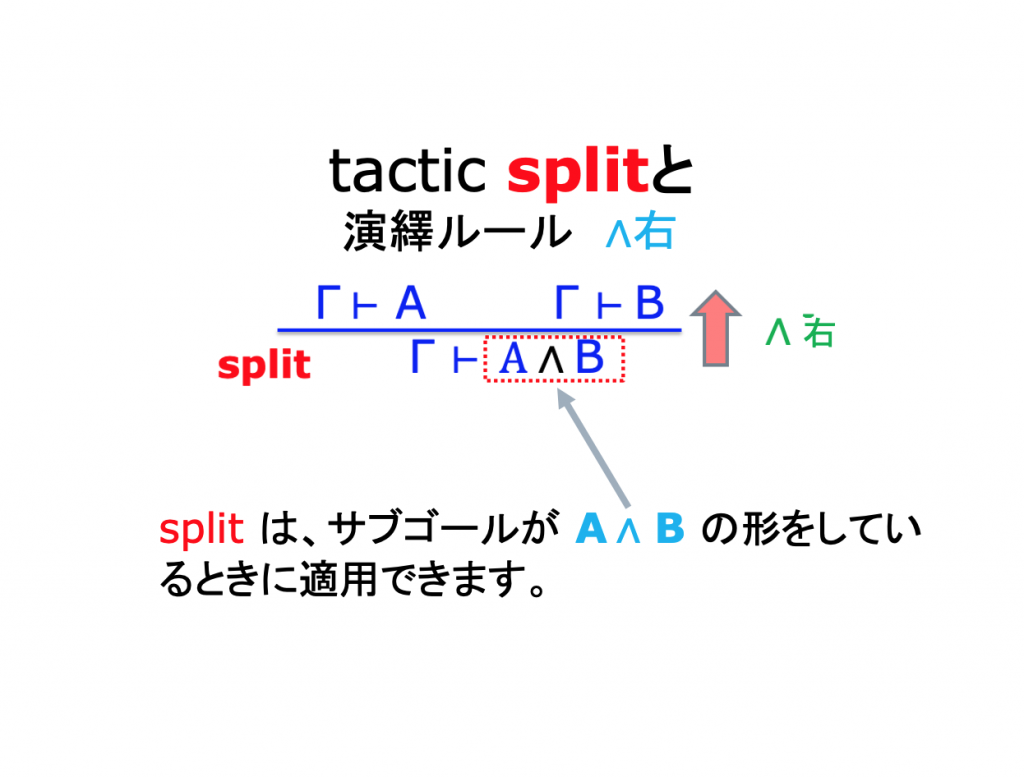
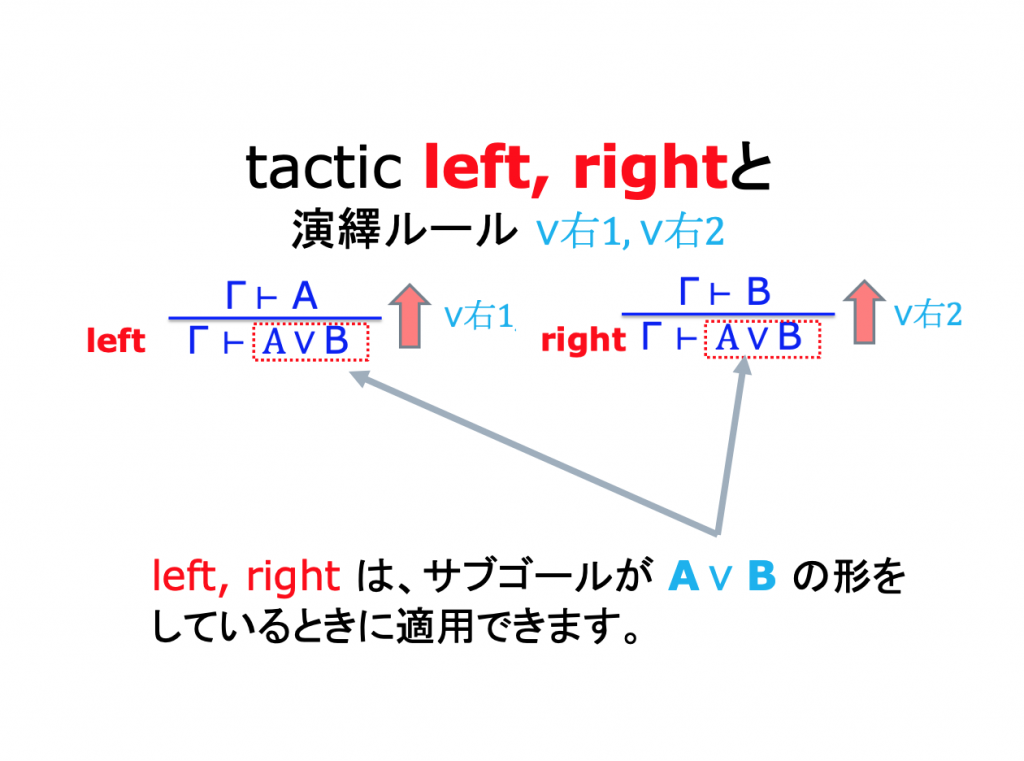
Sequent Calculusの演繹ルール

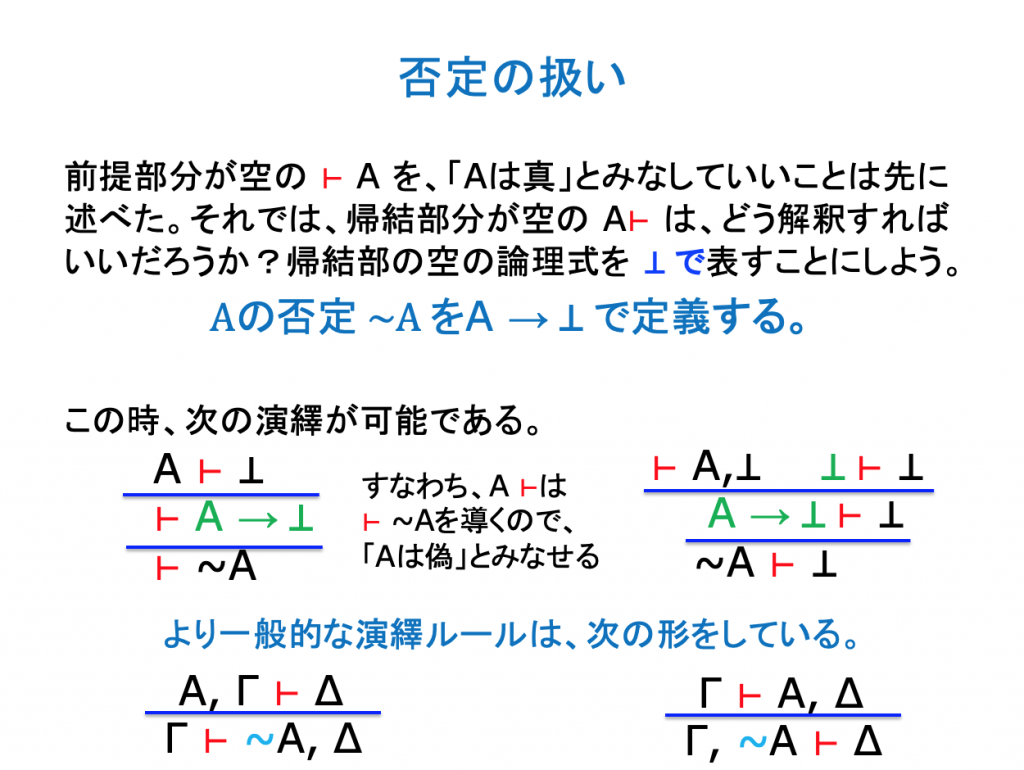

Sequent Calculusでの証明例
Part III Natural Deduction
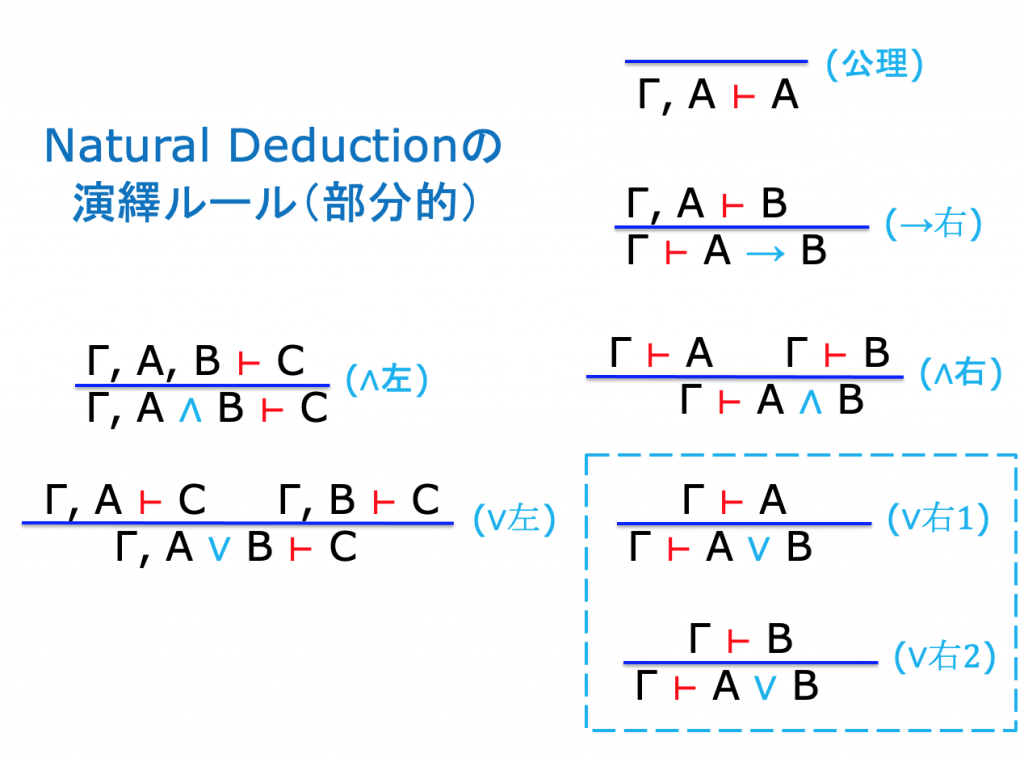
Natural Deduction


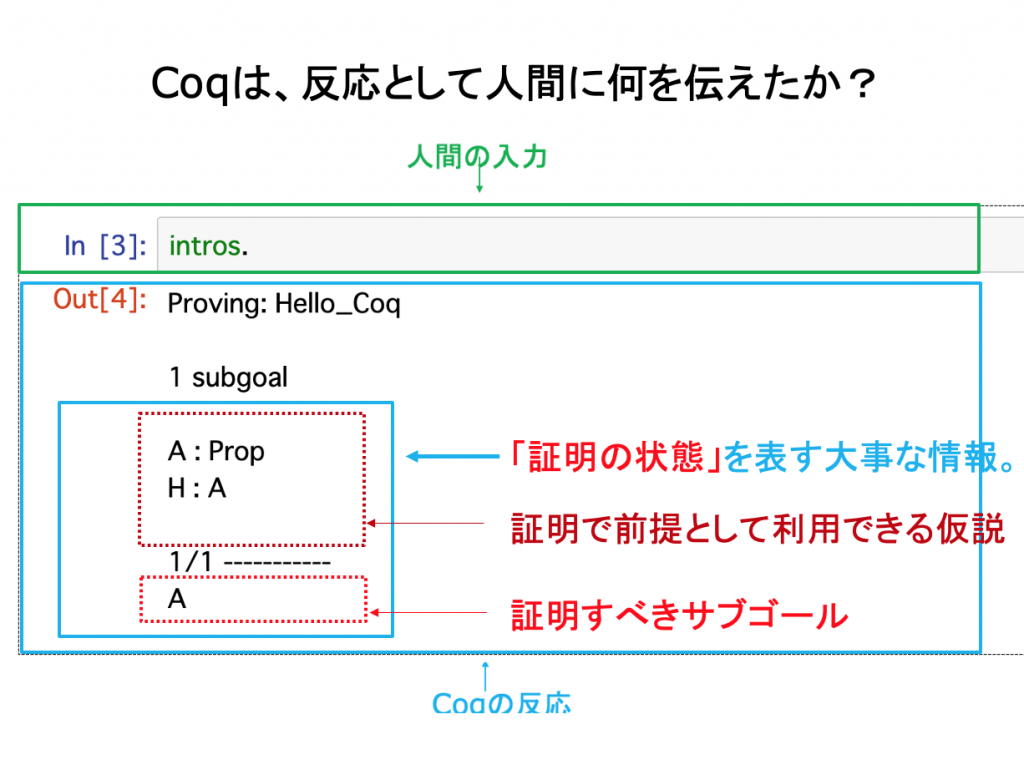
対話形証明システムとしてのCoq

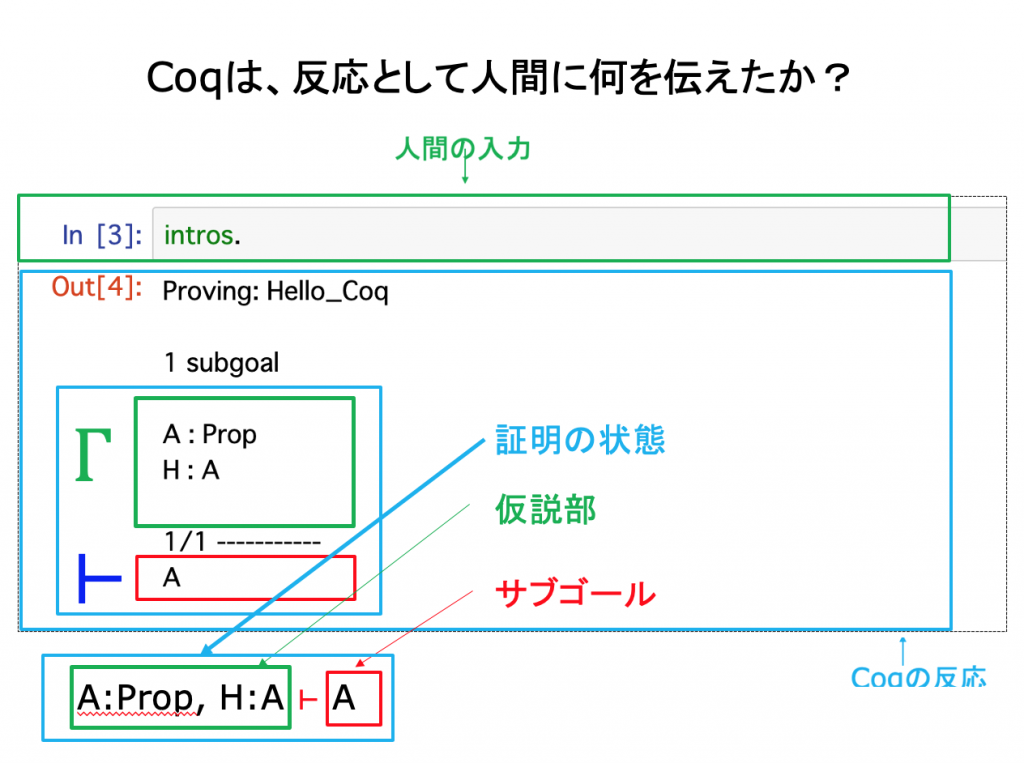
CoqとNatural Deduction