コンピュータ、数学の問題を解き始める

2022年3月2日 最終更新日時 : 2022年6月27日 MaruyamaFujio

目次

2022/03/26 マルレク 概要

3/26 マルレク「コンピュータ、数学の問題を解き始める」へのお誘い

Open-AI Theorem Prover

この2月に、 Open-AI はとても興味深い発表を行いました。彼らは、国際数学オリンピックのいくつかの問題をコンピュータを使って解いて見せたのです。例えば、2000年の数学オリンピックの問題は、こんな感じです。

問題
　 |x - 2| = p とする。 x < 2 の時、x - p = 2 - 2p となることを証明せよ。

証明
　 x < 2 なので、|x - 2| = - (x - 2)である。p = |x - 2| を使えば、x = 2 − p である。結局、x - p = 2− 2p となる。

この例は、高校生の数 I レベルのやさしい問題ですが、こうした問題をコンピュータが解くのは、画期的だと思います。論文には、この例をふくめて6つの例が紹介されています。

実際には、コンピュータは、形式的証明を返すのですが、ここで紹介したのは、「非形式的 Informal」な証明です。コンピュータは、Informal ボタンを押すと、こうした「非形式的」証明を返してくれます。形式的証明を非形式的証明へ要約・翻訳できるのも面白いです。

「数学オリンピックの形式的問題（のいくつか）を解く」
"Solving (Some) Formal Math Olympiad Problems"
https://openai.com/blog/formal-math/　

Deepmind Nature 論文

Deepmindは、数学へのAIの利用について、昨年12月、Natureにこんな論文を発表していました。それは、AIを利用することで人間の数学的直観を導くことができることを示して、数学者に向けてAIも使いみちがあると述べたものでした。

"Advancing mathematics by guiding human intuition with AI "　https://www.nature.com/articles/s41586-021-04086-x

今回のOpen-AIの発表は、そうした関心と方法の延長線上にあるものだと思います。

セミナーで伝えたいこと

セミナーでは、まず、Open-AI / Deepmind によるこうした動きを紹介しようと思います。それは、現在のAI技術の到達点を知る上で、重要なことだと思います。

ただ、今回のセミナーで伝えたいことは、もう一つあります。それは、こうした「成果」を、「ニューラル・ネットワーク」や「ディープ・ラーニング」、一般に AI 技術と言われるものの「成果」と単純に見做すべきではないということです。

丸山は、コンピュータ・プログラムが、もともと「論理=数学的推論」を行う能力を持っていると考えています。それは、いわゆるAI技術に基づいて「論理＝数学的推論」を実現しようというのとは異なる視点です。詳しくはセミナーで。

関連する論文 Deepmind AlphaCode

Deepmind は、2月に、数学オリンピックではなく、プログラム・コンテストの問題を解く取り組みを発表しています。

"Competition-Level Code Generation with AlphaCode
https://storage.googleapis.com/deepmind-media/AlphaCode/competition_level_code_generation_with_alphacode.pdf

Scott Aaronsonが、AlphaCodeを取り上げたblogのタイトルは、すこしひどいものでしたが、興味ある方は、ご一読を。

「下手くそな英語を話す犬としてのAlphaCode」
"AlphaCode as a dog speaking mediocre English"
https://scottaaronson.blog/?p=6288

セミナーの申し込み

セミナーの申し込み、受付を始めました。
次のページからお願いします。https://math-proof.peatix.com/

3/26 マルレク「コンピュータ、数学の問題を解き始める」講演資料

（ ダウンロード ）

3/26 マルレク「コンピュータ、数学の問題を解き始める」講演ビデオ

第1部 Open-AI Theorem Prover

第2部 Open-AI Theorem Proverは何を学習したのか？

第3部 数学者、証明にコンピュータを使い始める

第4部 形式的証明の背景と変化の意味を考える

セミナー解説blog

はじめに

( slide blog:「はじめに」)

第一部 Open-AI Theorem Prover

Open-AI Theorem Proverが証明したこと

( slide blog:「AIについての二つの見方」)

Open-AI Theorem Proverが行う証明

( slide blog:「誰が証明を行っているのか？」)

数学的証明の重要性とその難しさ

( slide blog:「Deep Learningの到達点と課題」)

難しさにどう立ち向かうか？

( slide blog:「セルフ・プレイに代わるもの」)

論文の結論にみるその「限界」の認識

( slide blog:「Open-AI Theorem Proverの限界」)

第二部 Open-AI Theorem Proverは何を学習したのか？

彼は、何を学習したのか？ (1) miniF2F-curriculum

( slide blog:「お勉強は大変だ」)

彼は、何を学習したのか？ (2) synth-ineq

( slide blog:「すごい！ でも、すこし違うかも」）

彼は、何を学習したのか？ (3) mathlib-train

( slide blog:「数学者、コンピュータを使い始める」)

第三部 数学者、証明にコンピュータを使い始める

数学者、コンピュータを使い始める

( slide )

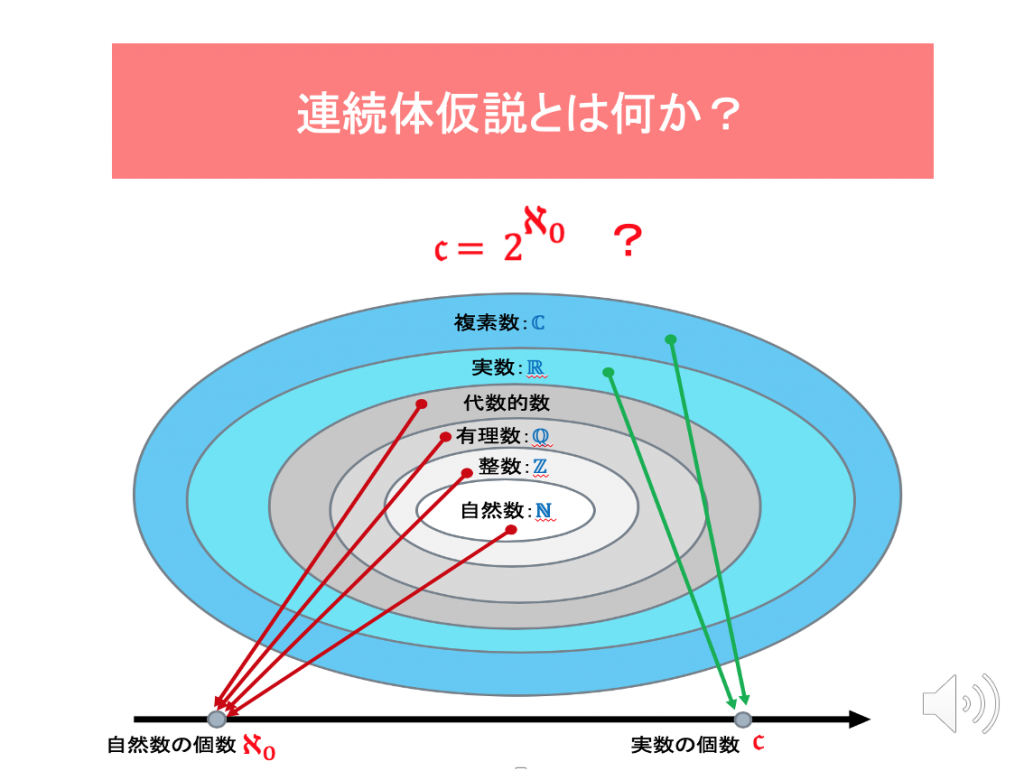
連続体仮説をコンピュータで解く

( slide blog:「感慨 -- 思えば遠くに来たもんだ」)

「連続体仮説」を自宅のマシンで「証明」してみたLog！

(ダウンロード)

Feit–Thompson定理の形式的証明

( slide blog:「数学者もブラックな冗談を言う」)

ケプラー予想の証明

( slide blog:「丸山、証明に失敗する」)

第四部 形式的証明の背景と変化の意味を考える

なぜ、証明にコンピュータを使うのか

( slide blog:「数学者も証明を間違える」)

数学的知の「累積性」

( slide blog:「巨人の肩の上の小人」)

Univatent Foundation

( slide blog:「数学のスタイルが変わる？」)

MaruLabo 関連資料

IT技術とCoqの世界 --証明 = プログラム = 計算の意味を考える

プログラムと論理

2のn乗の話（Turingマシンについて）

集合論入門

参考資料

  1. “Solving (Some) Formal Math Olympiad Problems”
    https://openai.com/blog/formal-math/?fbclid=IwAR1y4rK76c1BMN4FOgSLl3qPXk_cXxlZmIGnsy37wDsLdadRjbMiuoK4kFE
  2. “Formal Mathematics Statement Curriculum Learning”
    https://arxiv.org/pdf/2202.01344.pdf
  3. “Theorem Proving in Lean 4”
    https://leanprover.github.io/theorem_proving_in_lean4/
  4. "MINIF2F: A CROSS-SYSTEM BENCHMARK FOR FORMAL OLYMPIAD-LEVEL MATHEMATICS"
    https://arxiv.org/pdf/2109.00110.pdf
  5. "miniF2F-curriculum"
    https://github.com/openai/miniF2F/blob/statement_curriculum_learning/lean/src/statement_curriculum_learning/aopsbooks.lean
  6. "INT: AN INEQUALITY BENCHMARK FOR EVALUATING GENERALIZATION IN THEOREM PROVING"
    https://arxiv.org/pdf/2007.02924.pdf　
    https://github.com/albertqjiang/INT　
  7. "Lean mathlib"
    https://github.com/leanprover-community/mathlib
  8. "UniMath"
    https://github.com/UniMath/UniMath
  9. “A Formal Proof of the Independence of the Continuum Hypothesis”
    https://arxiv.org/pdf/2102.02901.pdf
    https://github.com/flypitch/flypitch/
  10. “A Machine-Checked Proof of the Odd Order Theorem”
    https://hal.inria.fr/hal-00816699/document
  11. "A formal proof of the Odd Order Theorem"
    https://github.com/math-comp/odd-order
  12. “A computer-checked proof of the Four Colour Theorem”
    http://www2.tcs.ifi.lmu.de/~abel/lehre/WS07-08/CAFR/4colproof.pdf
  13. "A formal proof of the Kepler conjecture"
    https://arxiv.org/pdf/1501.02155.pdf
  14. "Flyspec project"
    https://github.com/flyspeck/flyspeck
  15. “The Origins and Motivations of Univalent Foundations”
    https://www.ias.edu/ideas/2014/voevodsky-origins　
  16. UniMath GitHub
    https://github.com/UniMath/UniMath　
  17. "UniMath"
    https://www.math.ias.edu/vladimir/sites/math.ias.edu.vladimir/files/2016_09_22_HLF_Heidelberg.pdf
  18. "Univalent Foundations and the Large-Scale Formalization of Mathematics"
    https://www.ias.edu/ideas/2013/awodey-coquand-univalent-foundations
  19. Lean and its Mathematical Library
    https://leanprover-community.github.io/
資料種別
マルレク
テーマ
人工知能、形式手法
前の記事
「同じ」を考える -- Univalence Axiom 入門
2022年2月25日
次の記事
クラウドアプリケーションのためのオブジェクト指向分析設計講座 — 基本編 (9) 物理モデル
2022年3月20日