機械と人間が意味を共有する embeddingの世界を考える
セミナーへのお誘い
次回のマルレク「機械と人間が意味を共有するembeddingの世界を考える」へのお誘いです。
このセミナーは、前回のマルレク「機械の言語能力の獲得を考える」の続編になっています。
最初に、前回のセミナーを振り返ってみたいと思います。
前回のセミナー「機械の言語能力の獲得を考える」の振り返り
↑ 見出しクリックで前回セミナーの「まとめページ」へ
前回のセミナーのblog リストは、こちら をクリック。
前回のセミナーは、現在のAIの到達点を「機械の言語能力の獲得」と捉えるものでした。
理論史的には、語の意味の分散表現が文の意味の分散表現へと進み、それをベースとした「翻訳モデル」がAttention メカニズムの導入により発展します。 変化はさらに続きます。
Transformerを頂点とした「翻訳モデル」がencoder-only / decoder-only アーキテクチャーに分解・解体する中で、後者のアーキテクチャーの「勝利」として、「大規模言語モデル」が成立します。
「大規模言語モデル」の成功には、多くの要因があるのですが、前回のセミナーでは、その中で特に、三つの要因を挙げました。
- Next token predictionに特化したシンプルでスケーラブルなアーキテクチャーの採用
- Self-Supervised Learningによるインターネット上のラベルのない大量の文字データからのembeddingの生成能力
- In-Context learningとRetrieval-Augmented Generationによる、柔軟な機能拡張の能力
「機械の言語能力の獲得」という機械の能力の画期的な拡大を可能としたのは、技術的には、強力な「大規模言語モデル」の成立によるものです。
embeddingの働きを知ることの重要性
LLMの内部構造やその具体的な振る舞いについては、我々は既に多くのことを知っています。
ただ、LLMが Next token predictionマシンであるという認識と、それがコンテキストを含む言葉の意味を理解する能力として現れるという認識には、ギャップがあるように思います。
また、embeddingは、それ自身で既に「世界」についての情報を豊富に含んでいるように思えます。そうした特徴は外付けのRAGとは独立なものです。それは、embedding の生成メカニズムそのものにに根ざしているはずです。
僕は、機械が言語能力を獲得できたのは、人間のことばの意味をLLMがembeddingを通じて、理解できるようになったからだと考えています。
今回のセミナーでは、embeddingにフォーカスして、ただし、いろんな角度からembeddingの働きを考えていきたいと思います。
今回のセミナーでは、 「AIはなんでもできるかも」といった「AGI論」とは異なる、もう一つの別の視点を提供できると考えています。
前回のセミナー同様に、多くの皆様の参加を期待しています。
今回のセミナーの三つのトピック
今回の「機械と人間が意味を共有する embeddingの世界を考える」セミナーでは、次の三つのトピックを取り上げようと思います。
- lembeddingモデルとembedding プログラミング入門
- lembeddingがグローバルな検索の世界に与える影響
- lembedding論の新しい展開
以下、それぞれのトピックスの概要を紹介します。
embeddingモデルとembedding プログラミング入門


Language Model と Embedding Model
多くのAI ベンダーは、Language Model (LLM) と並んで Embedding Modelを提供しています。
Embedding Model
OpenAIの text-embedding-3-large, Googleのgemini-embedding-001をはじめとして、Cohere, Voyage AI, Mistral AI, Jina AI 等、多くのAIベンダーから多くのembeddingモデルが公開されています。オープンソースのHugging FaceのBGE(Beijing Academy of AI)もよく利用されているようです。
「embedding プログラミング入門」の目標
embedding モデルを利用したembedding プログラミングは、現在ではAIベースの検索・RAGの実装に広く利用されています。
今回のセミナーでのこのパートでは、 LLMを利用したコード開発の経験をもつIT技術者に、embedding プログラミングの基礎を、サンプルを通じて紹介することを目標にしています。
embedding プログラミングの経験は、LLMのより深い理解に、きっと役立つと思います。
embeddingがグローバルな検索の世界に与える影響
今回のセミナーのこのパートでは、AIの登場がグローバルなインターネット上の検索に与える影響を見ていきたいと思います。
検索の世界は、今、急速な変化の只中にあります。その変化を特徴づけるのは、機械が「ことばの意味を理解し始めた」という変化です。その変化は、「文字から意味への変化」と考えることができます。
「機械と人間が意味を共有するembeddingの世界」の登場が、検索の世界を変えようとしています。
21世紀のIT技術の二度目の大変化
それは、LLMの能力がRAGによって大きく拡大したという、狭いAI技術の変化の話ではないのです。
振り返ってみれば、GAFAM等のBig Techの成立に結果した21世紀初頭のITの世界の大きな変化は、Googleのグローバルな検索技術の登場によって先導されました。
その成功は、PageRank・MapReduceというアルゴリズムの実行を可能とするWebスケールの大規模分散システムと、「広告モデル」という新しいビジネス・モデルによって支えられたものでした。
四半世紀の時を経て、21世紀のIT技術・ITビジネスは二度目の大きな変化を迎えようとしています。
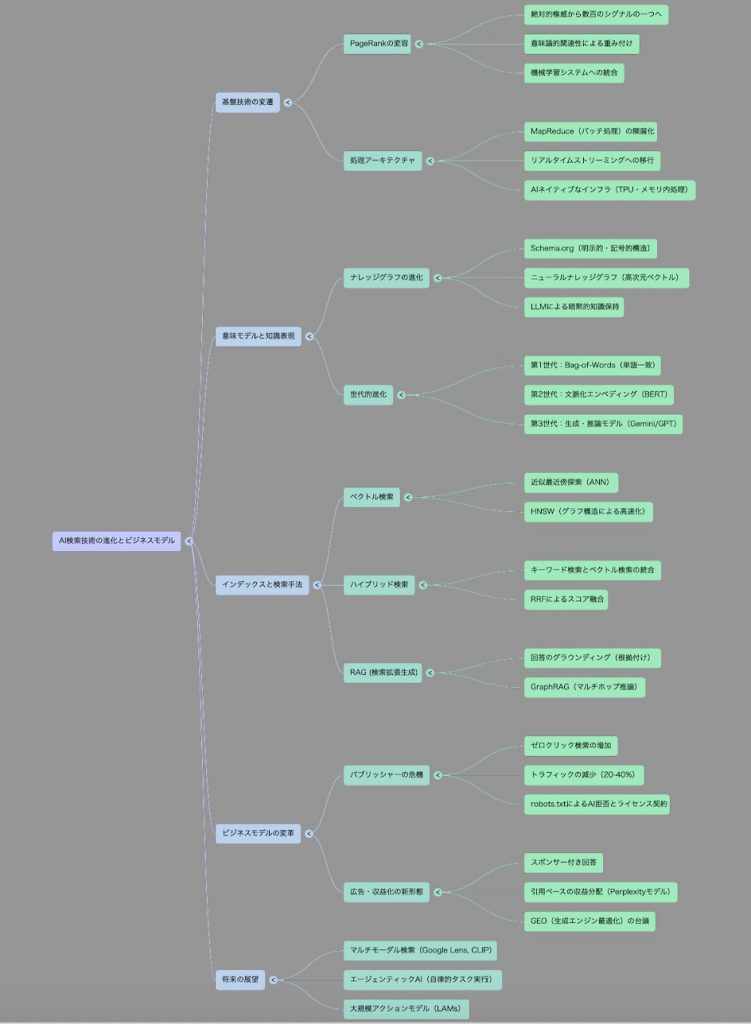
どのような変化を展望するのか
もっとも、予想される変化を現在のIT技術・ITビジネスの延長で考える必要はないと思います。
「機械の言語能力の獲得」は、機械にとっても人間にとっても歴史的な大事件です。より具体的に、「機械と人間が意味を共有するembeddingの世界」の進展は、機械にとっても人間にとっても重要な意味を持ちます。
それは、人類の情報共有と情報蓄積のスタイルが、大きく変わるだろうという展望を我々が持ちうることだと思います。
embedding論の新しい展開
今回のセミナーで取り上げたいと思っていることが、もう一つあります。前二つのパートと比べると、技術よりの内容です。
それは、LLMのある意味不思議な振る舞い、「LLMは、Next token predictionをするシステムだ」という還元論的特徴づけと、現実のLLMが示す柔軟で高度な意味理解能力の乖離がその典型的な例だと思いますが、そのメカニズムを、embedding論に遡って解明しようとする研究が活発に展開されていることです。
AnthropicのChristopher Olahらの「スパーズ・オートエンコーダー」 (Sparse Autoencoders) SAE理論が代表的な議論だと思います。
SAEとMI
この分野では、Olahらによる議論に触発された「機械論的解釈可能性」(Mechanistic Interpretability) MI理論も 興味深いものです。
これらの議論は、ブラックボックスとしてのLLMの振る舞いを、説明可能なものとして解明しようとするものです。同時に、こうした研究は、LLMの安全性を人間がキチンとコントロールする可能性を開くものでもあります。
個人的には、こうした研究は、VlassopoulosらのLLMの内部動作の解析と通じ、それをステップに BradleyのLLMのMagnitude論に通ずると考えています。
“Next token prediction” 描像を超える理論の探究
今回のセミナーの問題意識の一つは、LLMを「次のトークンを確率的に予測する」機械として捉える見方は、LLMの現実の振る舞いの説明としては、十分ではないのではというものです。
“LLM = Next token prediction Machine”という描像は、先のセミナーでも触れたように LLMの成功の技術的バックボーンの役割を果たしました。そのイメージは、一方で、「生成AI = 確率論的オーム」という誤解を生み出し、他方ではAI研究者を含む多くの人に、「LLM = ブラックボックス」であることを印象付けました。ただ、後者の認識は「誤解」ではありません。
“Next token prediction” 描像を超えるLLM理論の探究は、現在のLLM研究のもっとも興味深い領域だと思います。
基本的には、カテゴリー論を使ってこの問題にアプローチする流儀と、AI研究者の「ブラック・ボックス問題」に切り込もうとする流儀の、二つのアプローチがあります。興味深いのは、両者の研究がクロスする状況が生まれていることです。
カテゴリー論的アプローチ
カテゴリー論的アプローチの代表者は、Tai−Danae Bradleyです。
彼女の 「co−presheaf 意味論」は、画期的なものです。
Bradley
彼女の最近の研究は、次の二つの点で大きな前進を遂げています。
・LLMの内部の確率計算の精緻な分析。プロンプトxが与えられた時、LLMが出力yを返す確率π( y | x )の計算式を与えました。
・その上で、「確率」を「距離」に変換し、「意味の幾何学」への道を開きました。
音声概説 Bradley1
音声概説 Bradley2
Vlassopoulos
Vlassopoulosは、基本的にBradley と同じアプローチをとっています。
興味深いのは、彼の議論は、SAE理論の「Superinpose」の議論と親和性が高いと、僕は感じています。

