Tensor Network入門
誰でも分かるテンソル・ネットワーク入門
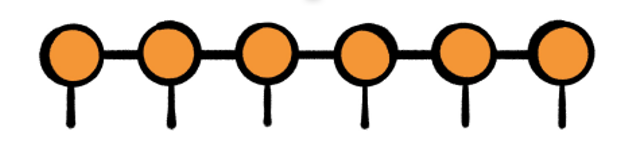
今、テンソルを多数並べて、一つのネットワークを作る「テンソル・ネットワーク」という技術が、物理学でもディープ・ラーニングでも、いろんなところで活躍しています。
「ちょっと待って。何の話をしているの? テンソルを並べると言っても、そもそもテンソルが何かわからないし。」
「テンソル」というのは、スカラーやベクトルや行列といった数学的概念を一般化したものです。
「ベクトルは、イメージはある。矢印のことだろ。行列はどっかで習ったような気がするけど、行列の掛け算、むづかしかった。嫌になった。スカラー、聞いたことないな。わからないことを一般化すると、わかりやすくなるの? わからないままでしょう。」
スカラーは、数字のことです。ベクトルは、数字が並んだものです。数字同士を掛け算できるように、ベクトル同士も、掛け算できるんですよ。それをベクトルの「内積」と言います。
「ベクトルの内積? もういいよ、興味ないから。普通の掛け算できれば、日常生活じゃ十分じゃない? 電卓だってエクセルだってあるし。」
どうやら、「テンソル・ネットワーク」導入に失敗したようです。中身に入る前に。
ただ、それは残念なことだと思います。というのも、テンソル・ネットワークの基本的な考え方は、行列の掛け算よりずっとやさしいからです。多分、小学生でも理解できると思います。
皆さんも、テンソル・ネットワークの世界、のぞいてみませんか?
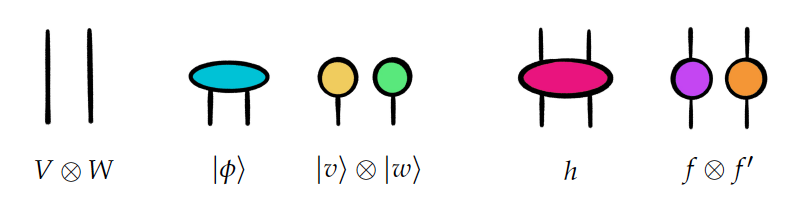
このセッションは、セミナー「密度行列 ρ で理解する確率の世界」https://www.marulabo.net/docs/density2/ の一部なのですが、少し説明が長くなってしまったので、初等的なところだけをまとめて、別ページ を作りました。
Bra-Ket記法は Diracのアイデアによるものですが、Tensor Networkは Penroseのアイデアを発展させたものです。
ベクトルを図形で表す
( slide-pdf )
行列を図形で表す
( slide-pdf )
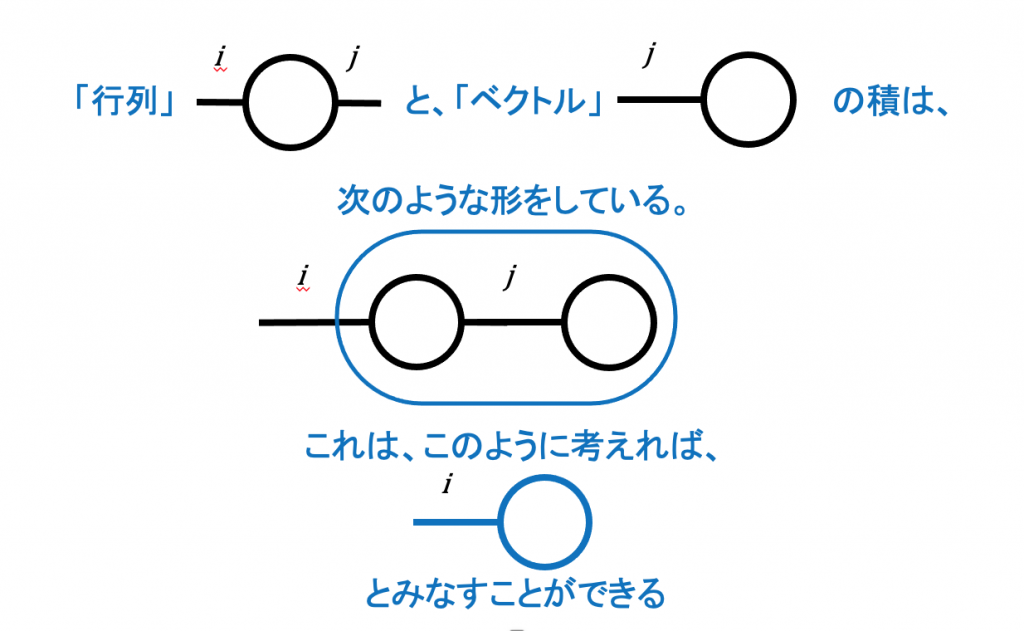
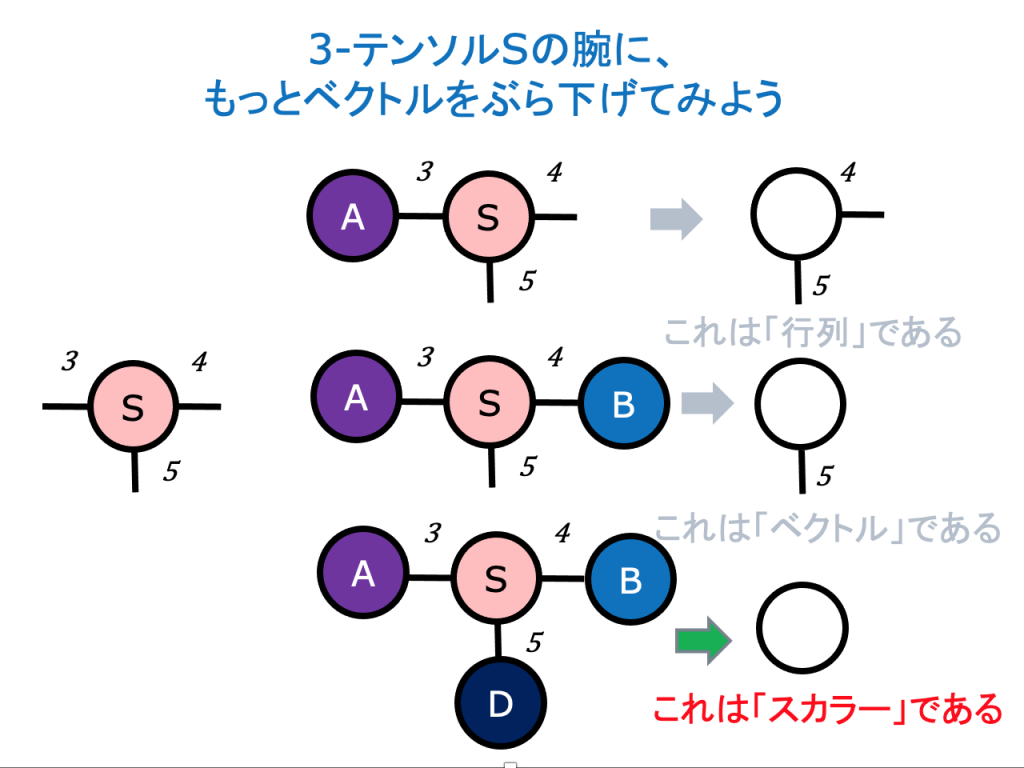
3-テンソル
( slide-pdf )
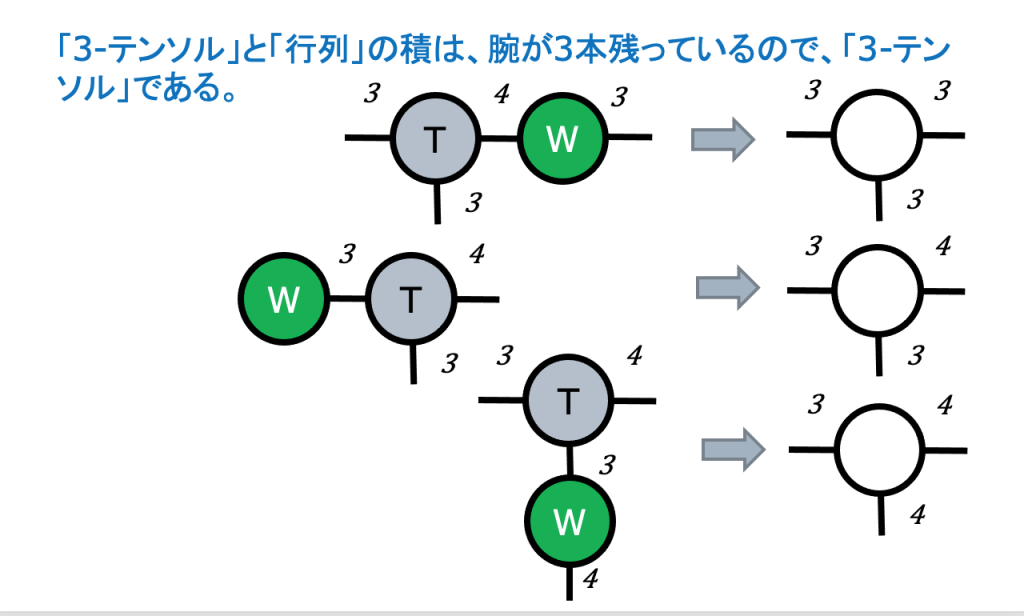
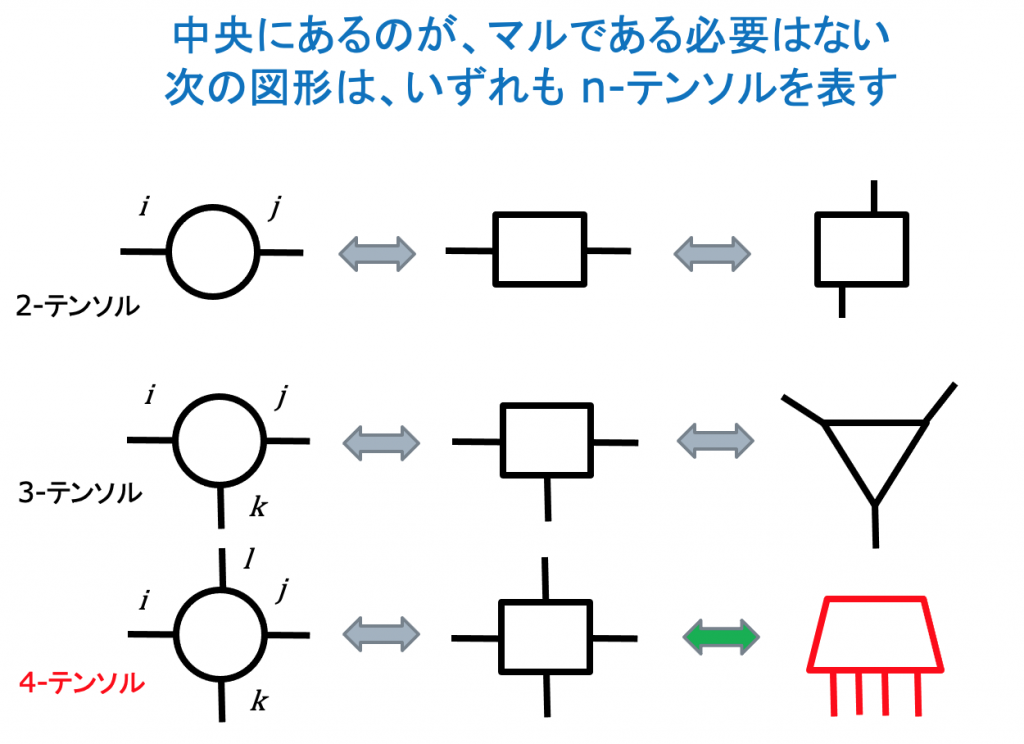
テンソルを図形で表す
( slide-pdf )
テンソルのContraction
( slide-pdf )
Tensor Networkの基礎 — テンソル積の表現
( slide-pdf )
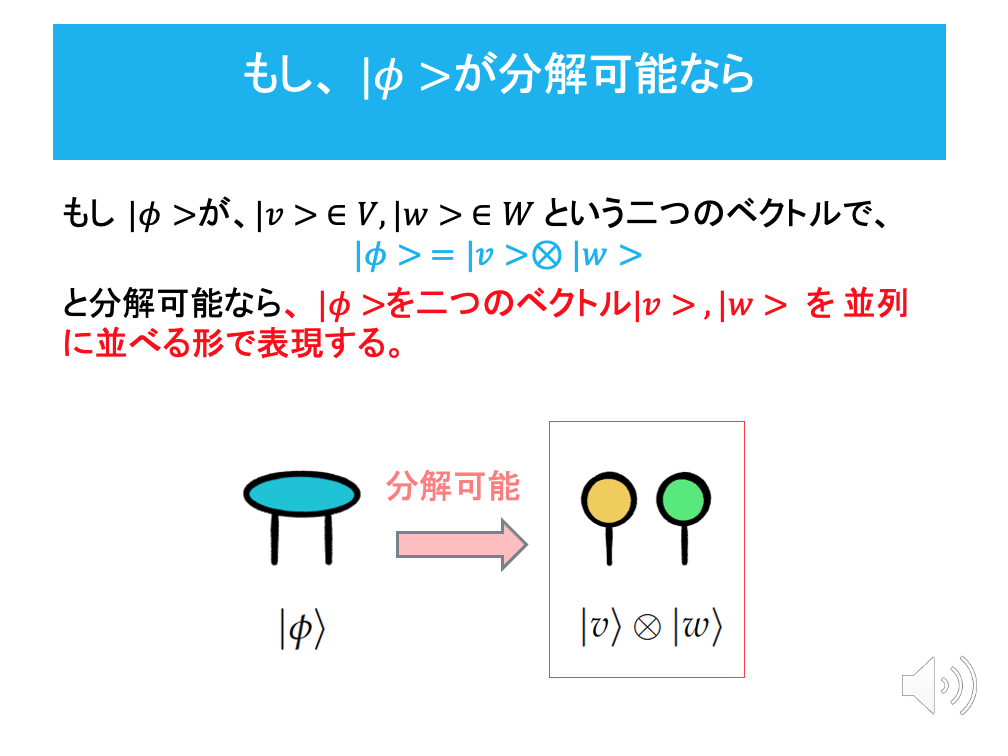

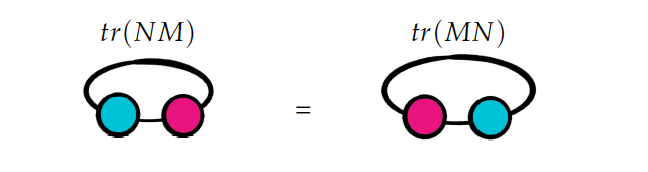
こんな使い方に発展するんです
今回は、ここまでです。
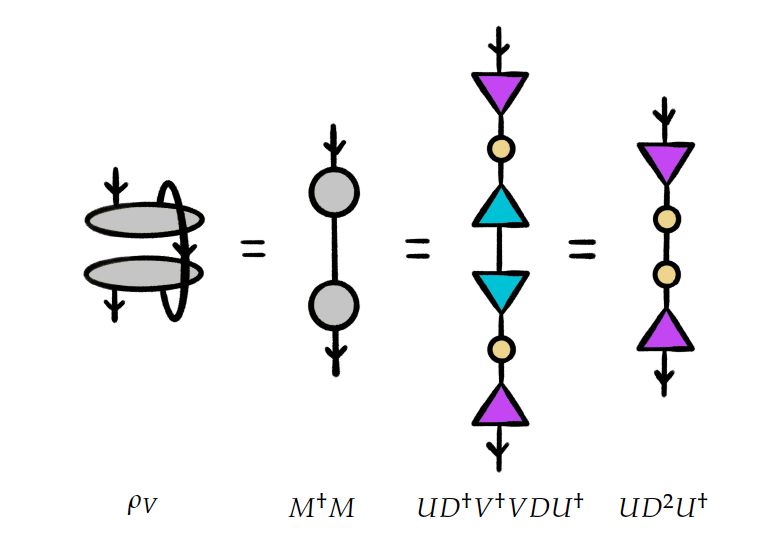
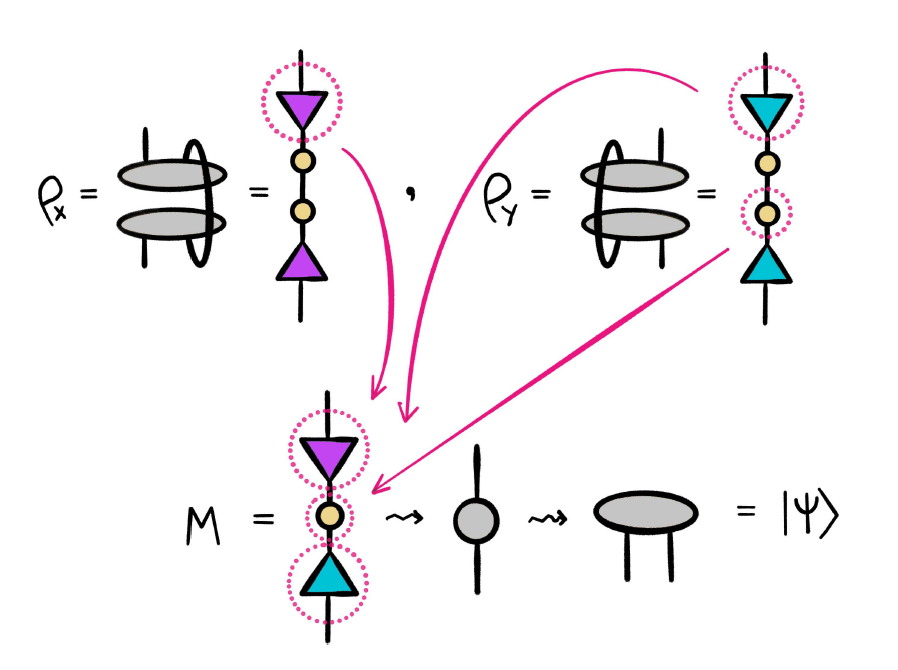
これが、次のような使い方に発展します。「密度行列 ρ で理解する確率の世界」をご覧ください。