「カテゴリー論入門」のセミナーを、2月のマルゼミから始めたいと思っています。
「カテゴリー論入門」のセミナーは、次のような構成を考えています。
第一回:String Diagramを学ぶ
「量子過程を図解する String Diagram 入門」
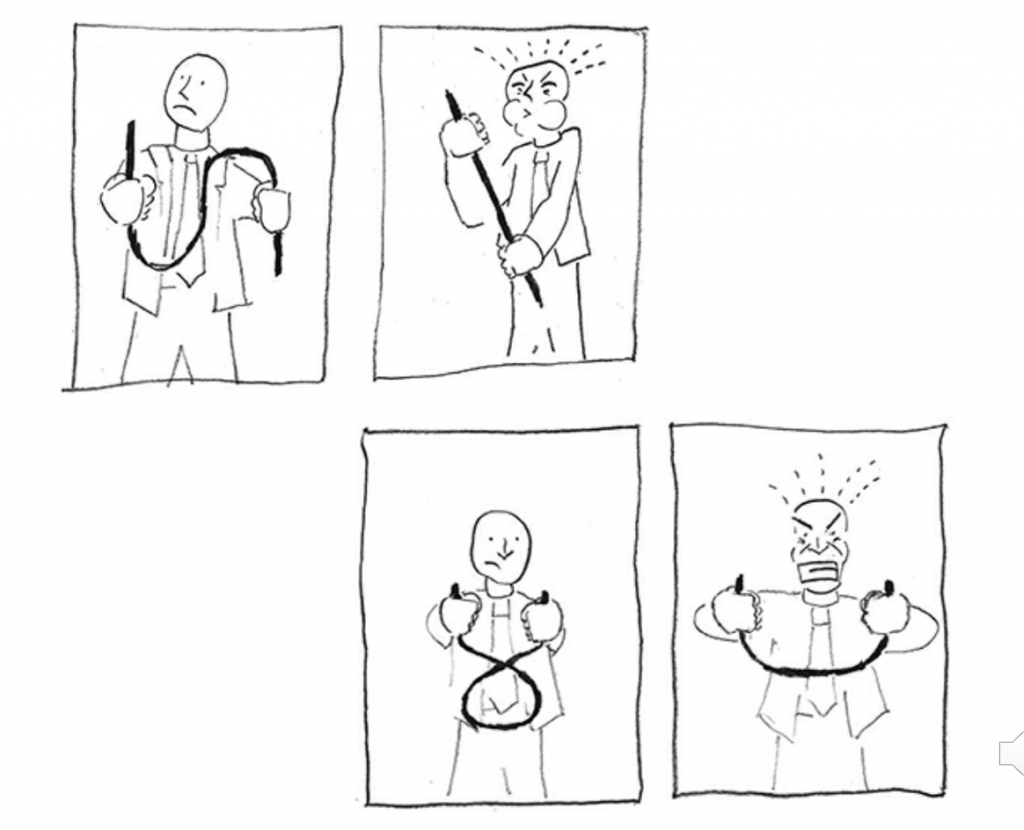

カテゴリー論の最初の入り口として、量子の世界を図形で表現しようとするString Diagram という手法を紹介したいと思います。
参考文献
Bob Coecke,Aleks Kissinger: “Picturing Quantum Processes”
https://www.amazon.co.jp/-/en/Bob-Coecke/dp/110710422X
第二回:String Diagramの数学的基礎
「String DiagramとSymmetric Monoidal Category」
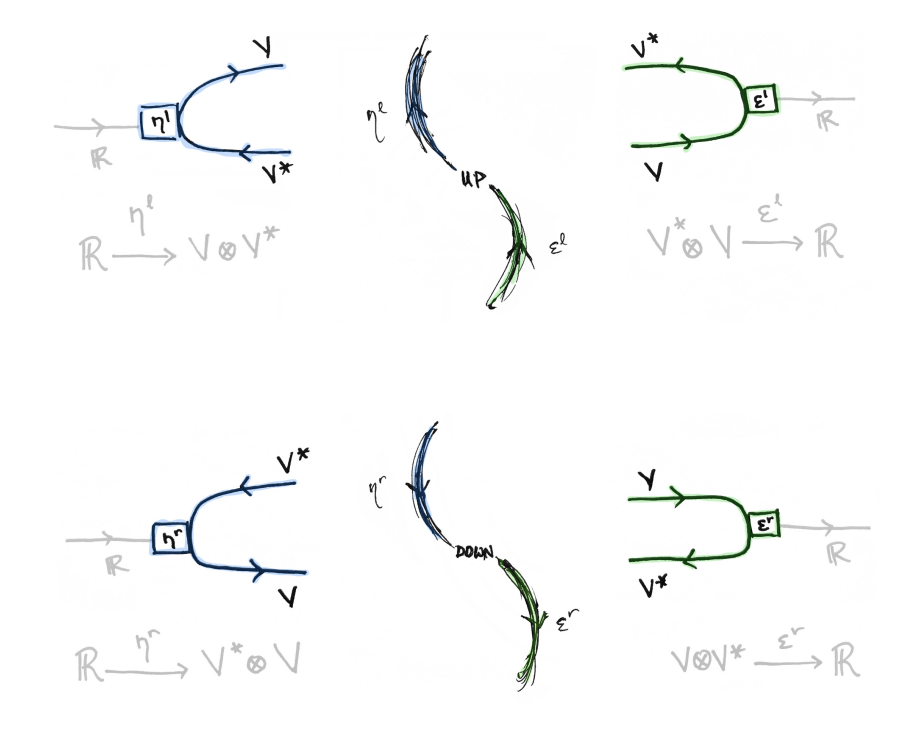
ここでは、先に見たString Diagramが、カテゴリー論の応用であることを見ていきます。
カテゴリー論の数学的な説明は、この回から始まります。
参考文献
Tai-Danae Bradley: “What is applied category theory?”
https://arxiv.org/pdf/1809.05923.pdf
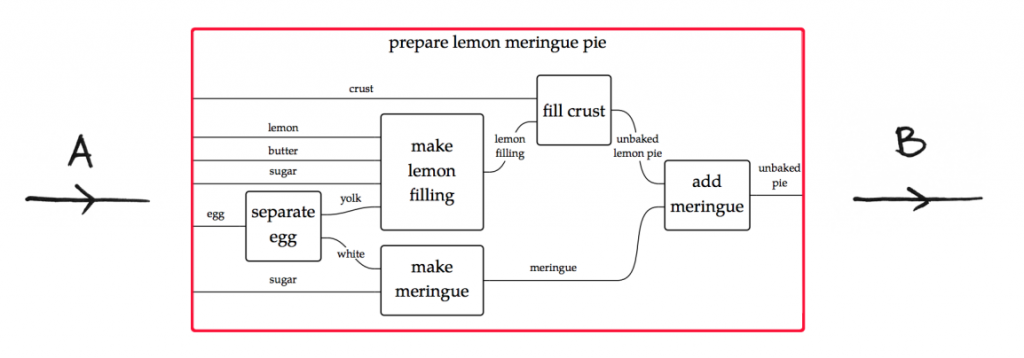
Brendan Fong ,David I. Spivak :”Seven Sketches in Compositionality: An Invitation to Applied Category Theory”
https://arxiv.org/pdf/1803.05316.pdf
第三回:カテゴリー論の応用の射程
「A Rosetta Stone」
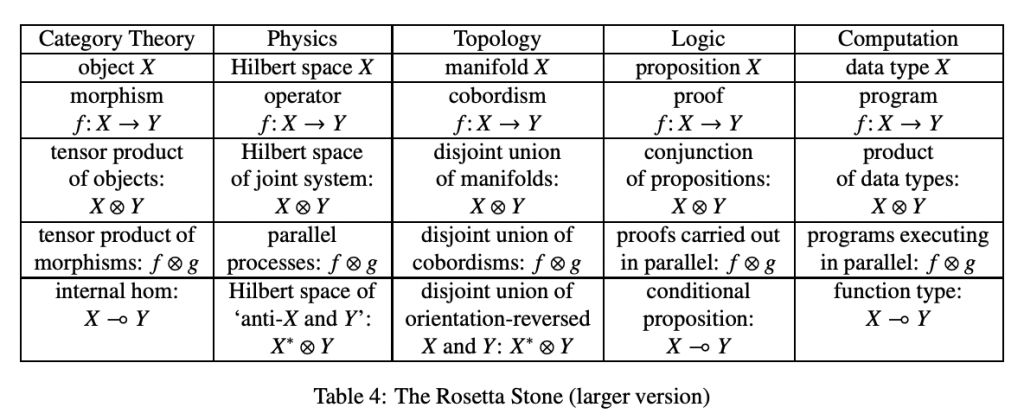
カテゴリー論の応用の可能性を大きく拡大した、John Baezの仕事を紹介します。
参考文献
John Baez,Mike Stay :”Physics, Topology, Logic and Computation:”A Rosetta Stone” https://math.ucr.edu/home/baez/rosetta.pdf
第四回:数学の基礎とカテゴリー論
「Univalent foundationsとHomotopy Type Theory」

21世紀に入って、カテゴリー論は数学を基礎づける理論として新たな注目を集めます。
こうした動きを主導したVoevdskyの仕事を紹介します。
参考文献
Vladimir Voevodsky:”Foundations of Mathematics:their past, present and future” https://www.math.ias.edu/vladimir/sites/math.ias.edu.vladimir/files/2014_09_Bernays_3%20presentation.pdf