String Diagram を学ぶ — カテゴリー論入門 (1)

2022年2月3日 2022年5月29日 MaruyamaFujio

2022/02/26 マルゼミ「String Diagram を学ぶ — カテゴリー論入門 (1)」概要

2月のマルゼミでは、String Diagramについて学びます。具体的には、Bob Coeckeの “Picturing Quantum Processes”に依拠して、量子過程を図解する手法としてのString Diagramを学びます。
このセミナーは、今後、継続的に開催される「カテゴリー論入門」シリーズの第一回目として開催されます。詳しくは、「「カテゴリー論入門」セミナーについて」を参照ください。

セミナー概要「はじめに」から

String Diagram とは何か？

String Diagramは、直観では理解しにくい（むしろ直観に反した）量子過程の諸特徴を、数式を使わずに「図式 Diagram」を使って、直観的に理解することを可能にする新しい方法です。それは、図式を使うことにはとどまらない、従来のアプローチにはない優れた特徴を持っています。

「状態」と「過程」

フォン・ノイマンによって定式化された従来のアプローチでは、量子の「状態」をヒルベルト空間上のベクトルとして捉えます。また「観測可能量」は、ヒルベルト空間上のエルミート演算子に対応し、実際に観測される「状態」の確率は、ボルンのルールで与えられます。それに対して、String Diagramでは、全てのものが「過程 process」として統一的に捉えられます。

「重ね合わせ」と「エンタングルメント」

従来の定式化は、量子論の主要な特徴を「状態」の「重ね合わせ」と「観測」の「確率解釈」として捉えます。ただ、それは、「エンタングルメント」のような量子過程に、直接フォーカスしているわけではありません。String Diagramは、エンタングルメントのような「不可分離性 non-separability」を量子論の特徴として捉えようとします。

「量子過程」と「情報過程」

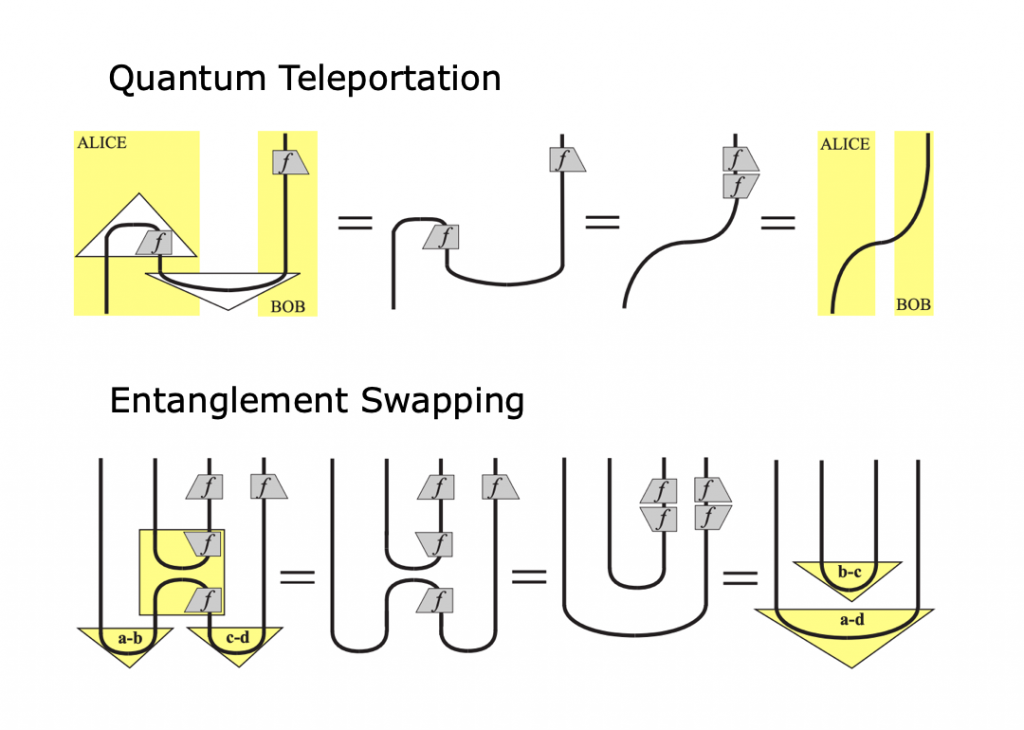
従来のアプローチでは、量子過程の情報的側面には、ほとんど関心が向けられていませんでした。String Diagramでは、量子テレポーテーション、エンタングルメント・スワップメント等の量子過程の情報的側面に大きな関心が寄せられています。

「数式」と「図式」

「数式」の方が「図式」より、正確で情報量が多いというのは、ある種の思い込みです。
String Diagramの「図式」は、「数式」で表現される抽象的なカテゴリ〜論と同値です。oString Diagramの「図式」は、直観的で分かりやすいだけでなく、それを理解するのに、カテゴリー論を学ぶ必要もありません。