量子アルゴリズム入門 — 量子フーリエ変換を学ぶ
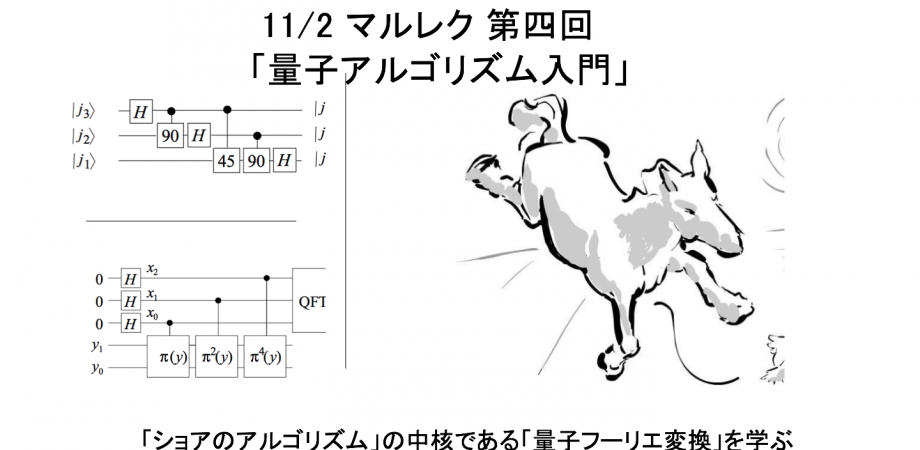
2018/11/02「量子アルゴリズム入門 — 量子フーリエ変換を学ぶ」概要
今回のマルレクのテーマは、「量子アルゴリズム入門」です。
メディア的には、量子コンピュータへの関心を訴求する一番大きなポイントは、Google, IBM, Microsoft をはじめとする大手ITベンダーが、50-100qubitの中規模の量子コンピュータを実際に作り上げる取り組みを精力的に進めていることが大きいかもしれません。それは、確かに重要な変化です。
ただ、現在起きている変化は、それだけではありません。量子コンピュータをハードウェアだとすると、その上で走るソフトウェアに相当する「量子アルゴリズム」の研究・開発が、爆発的に進んでいます。
90年代にショアの素因数分解のアルゴリズムが発表された時は、ハードウェアの実現の見通しとは独立に、アルゴリズムそのものに、非常に大きな関心が集まりました。むしろ、そこで膨らんだ期待が、ハードウェア上の制約で、その実現がすぐには難しいと分かった時に、量子コンピュータそのものに対する失望に変わったように思います。
冒頭にも書きましたように、量子コンピュータのデバイスとしての実現可能性をめぐる状況は、90年代とははっきり変わって来ています。それ以上に重要なことは、この分野のイノベーションは、ショアのアルゴリズムの発見がそうであったように、先行する理論的探求によってに牽引されるということです。
現在、多くの研究者を巻き込み、深い結果が出て来ている量子アルゴリズムの研究動向は、量子コンピュータの未来を占う上で、決定的と言っていい重要な意味を持っています。
今回のマルレクでは、量子アルゴリズムの「金字塔」といっていい、ショアのアルゴリズムの中核である「量子フーリア変換」のやさしい解説を行いたいと思います。この間、展開して来た「紙と鉛筆で学ぶ量子情報理論演習」の内容は、きっと役にたつと思います。
古典的フーリエ変換
フーリエ級数とフーリエ係数

なめらかではない矩形波や鋸波も、次のように、sin の和として表わすことができる。https://upload.wikimedia.org/wikipedia/commons/1/1a/Fourier_series_square_wave_circles_animation.gif
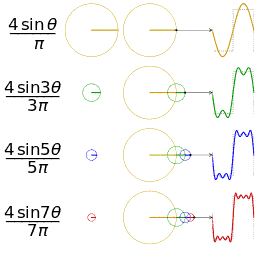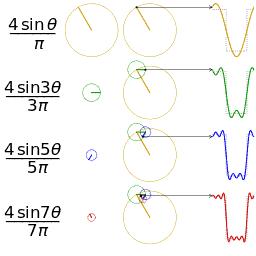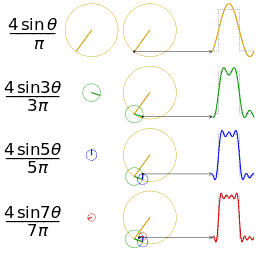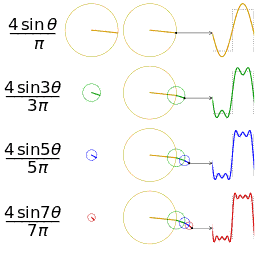
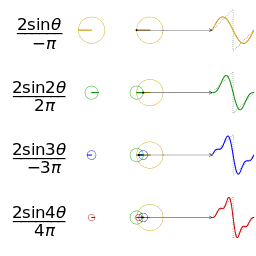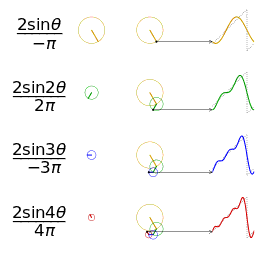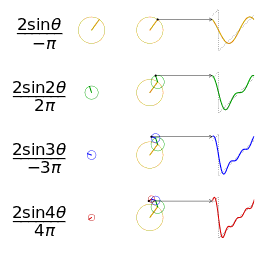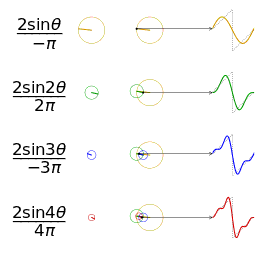
フーリエ変換
関数fのフーリエ級数展開表示を、その周波数成分を取り出した周波数領域表示に変えることをフーリエ変換と呼び、𝑓 ̂で表す。https://ja.wikipedia.org/wiki/%E3%83%95%E3%83%BC%E3%83%AA%E3%82%A8%E5%A4%89%E6%8F%9B#/media/File:Fourier_transform_time_and_frequency_domains_(small).gif
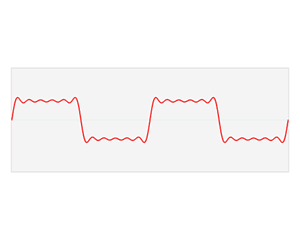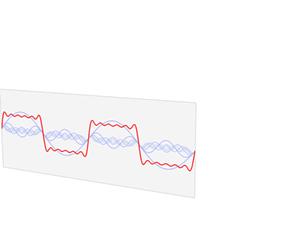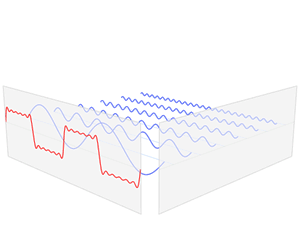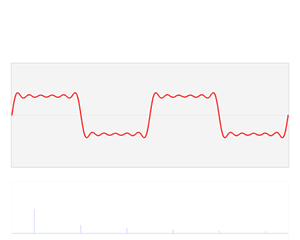
Sines and cosines form an orthonormal set, as illustrated above.
The integral of sine, cosine and their product is zero
(green and red areas are equal, and cancel out)
when m, n or the functions are different, and pi only if m and n
are equal, and the function used is the same.


フーリエ級数・フーリエ変換を複素数で考える
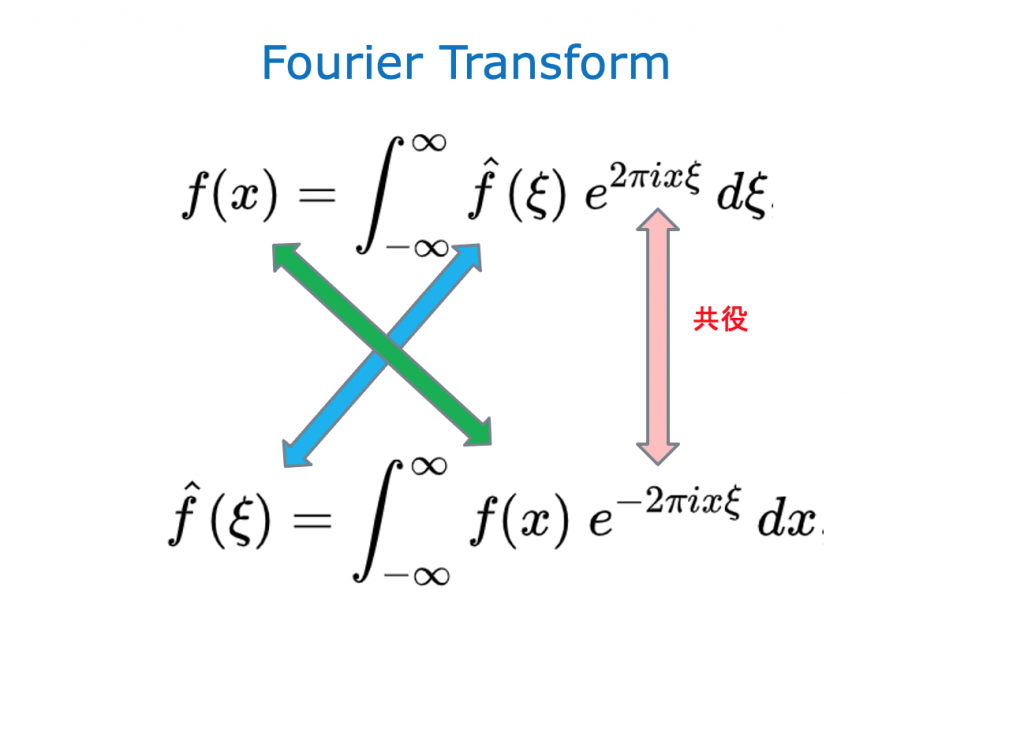
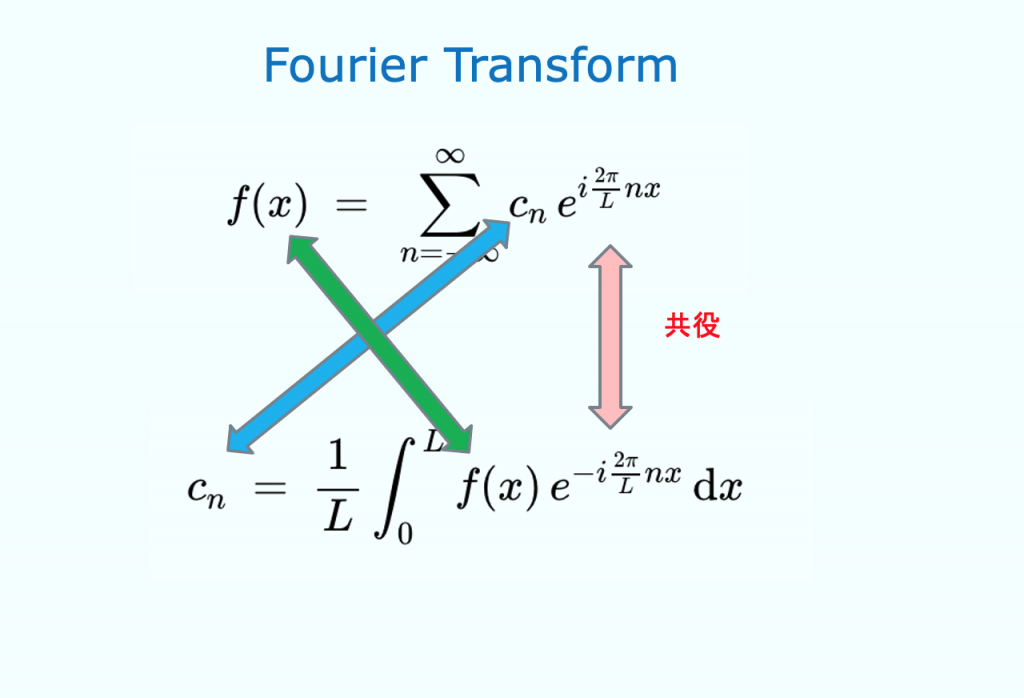
講演資料 (ダウンロード)
ディジタル フーリエ変換
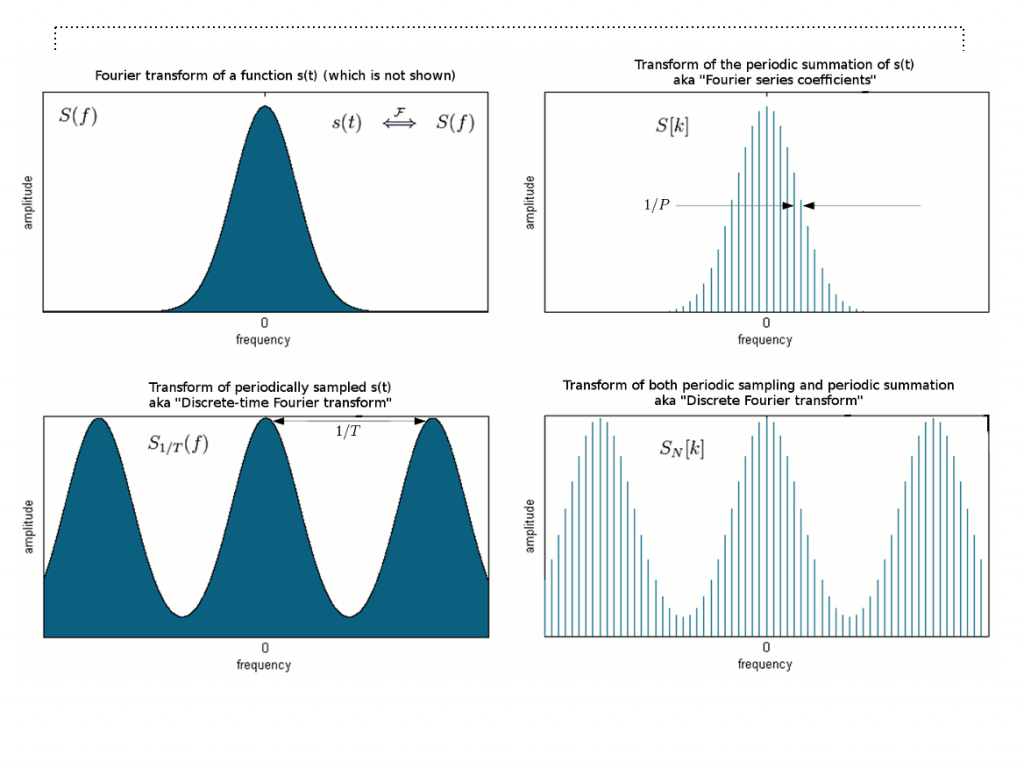
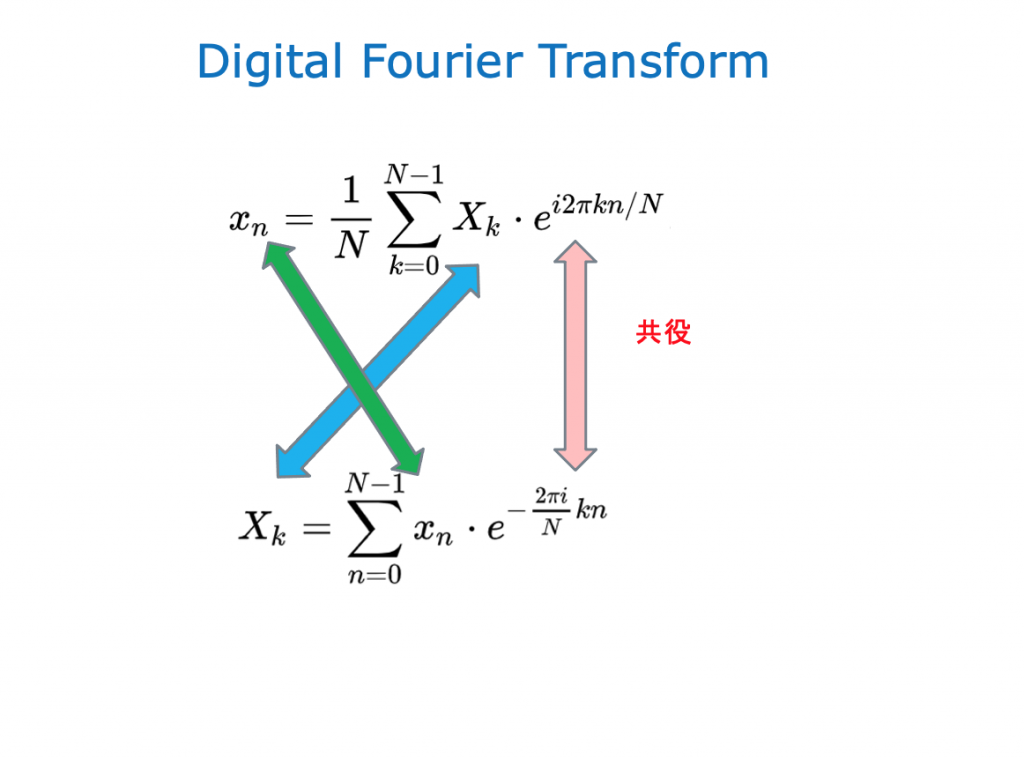

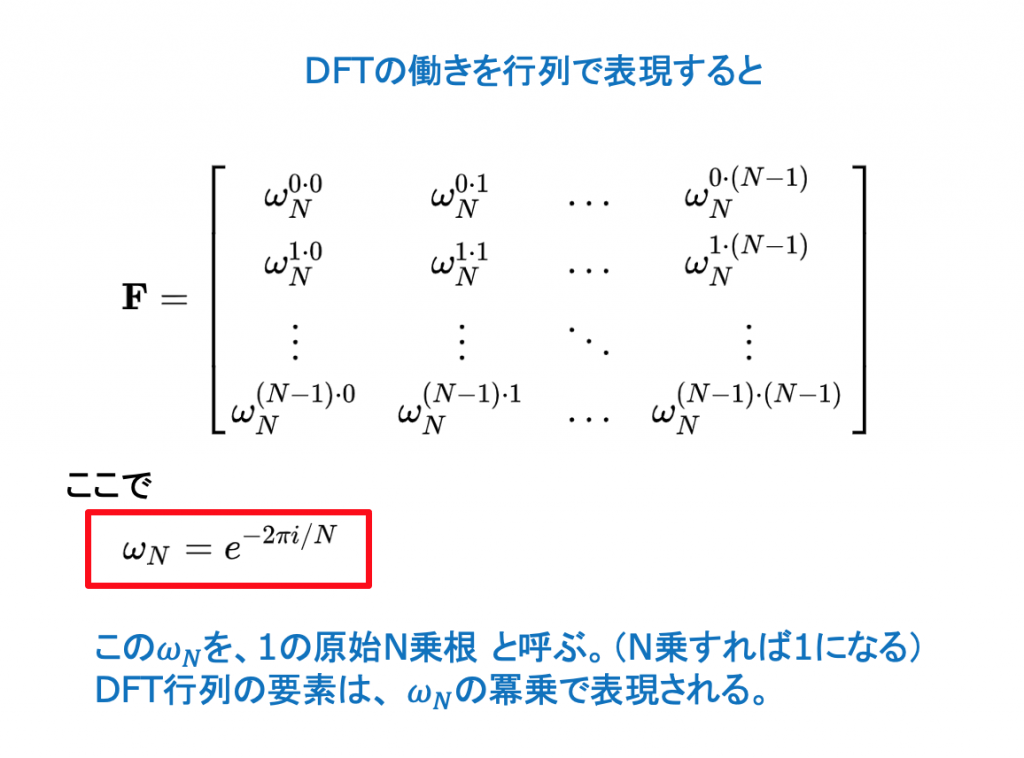
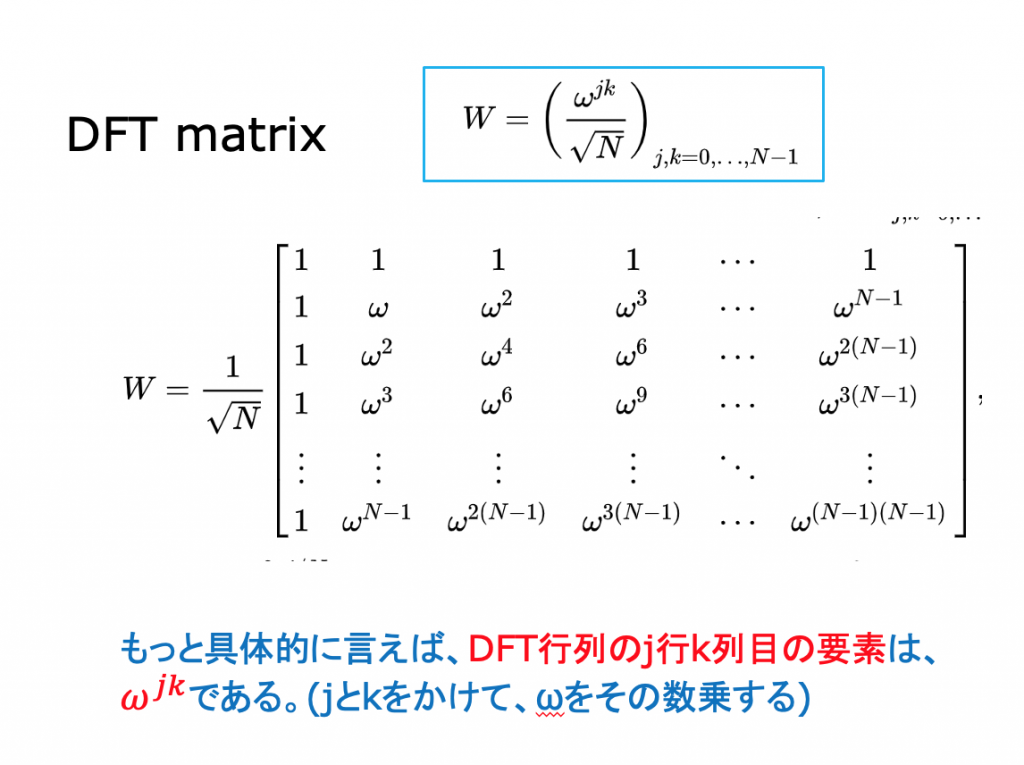

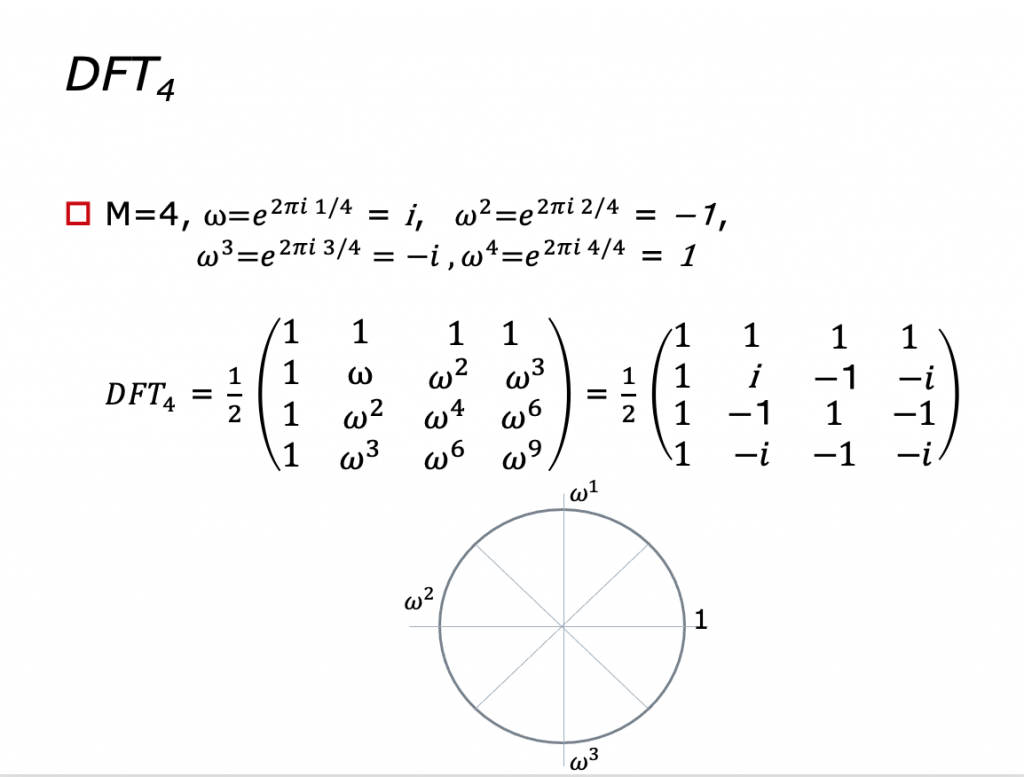

講演資料 (ダウンロード)
高速フーリエ変換
Fast Fourier transforms are widely used for many applications in engineering, science, and mathematics. The basic ideas were popularized in 1965, but some algorithms had been derived as early as 1805.[3] In 1994, Gilbert Strang described the FFT as “the most important numerical algorithm of our lifetime”[4][5] and it was included in Top 10 Algorithms of 20th Century by the IEEE journal Computing in Science & Engineering.[6]
The DFT is obtained by decomposing a sequence of values into components of different frequencies.[3] This operation is useful in many fields (see discrete Fourier transform for properties and applications of the transform) but computing it directly from the definition is often too slow to be practical. An FFT is a way to compute the same result more quickly: computing the DFT of N points in the naive way, using the definition, takes O(N2) arithmetical operations, while an FFT can compute the same DFT in only O(N log N) operations. The difference in speed can be enormous, especially for long data sets where N may be in the thousands or millions.
In practice, the computation time can be reduced by several orders of magnitude in such cases, and the improvement is roughly proportional toN / log N. This huge improvement made the calculation of the DFT practical; FFTs are of great importance to a wide variety of applications, from digital signal processing and solving partial differential equations to algorithms for quick multiplication of large integers.
https://en.wikipedia.org/wiki/Fast_Fourier_transform
講演資料 (ダウンロード)
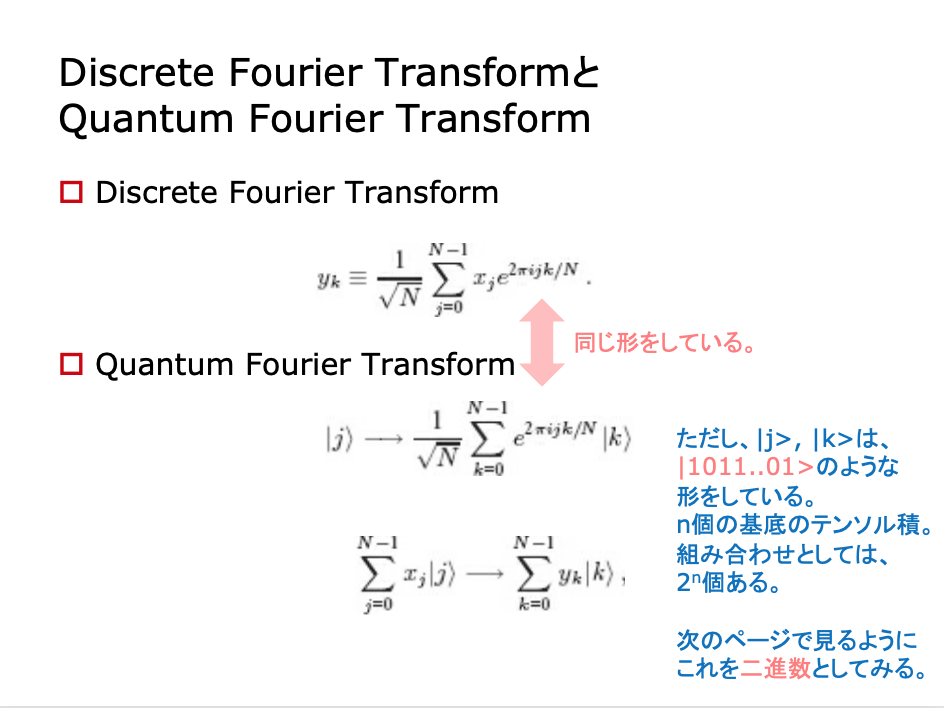
量子フーリエ変換
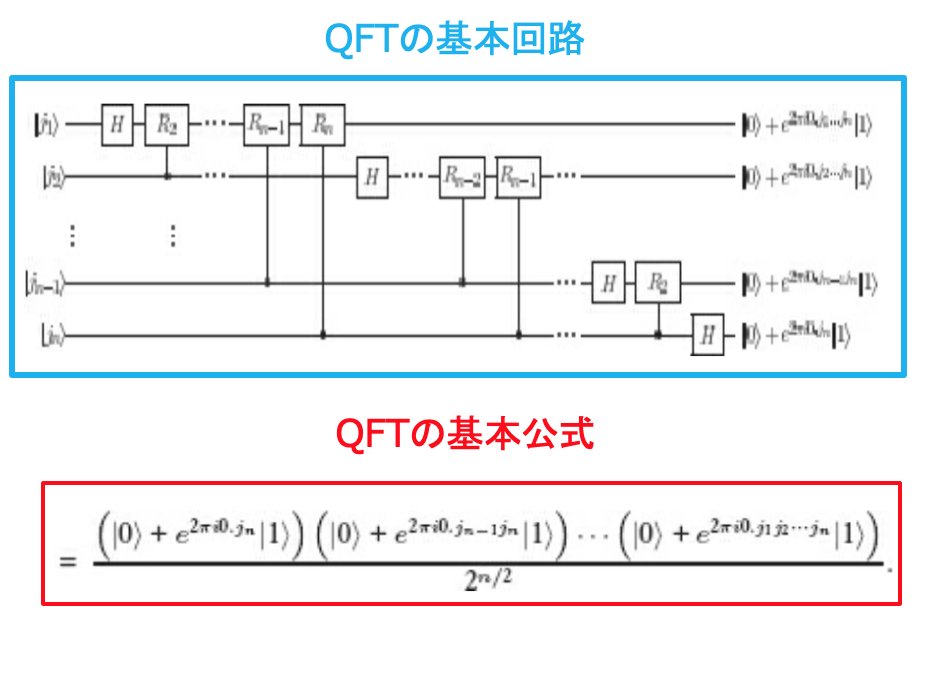
QFTをQuantum Gateで実装する
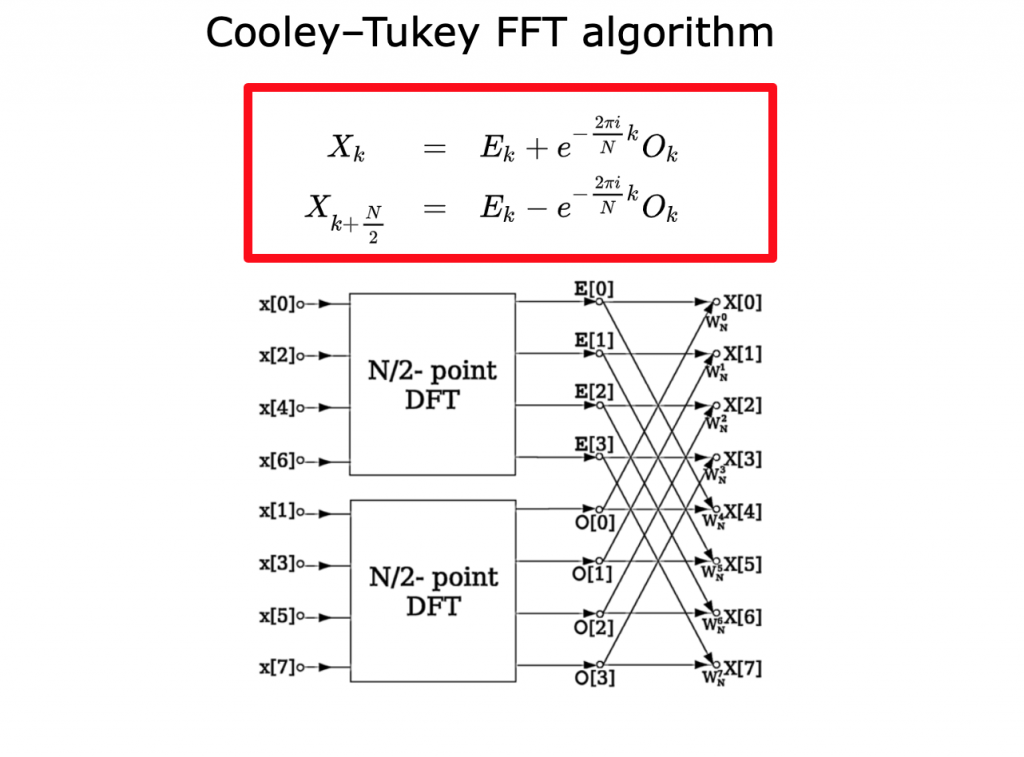
QFTは、FFTに動機付けられているので、同じようなステップで進むのだが、いくつかの点で実装が異なっている。
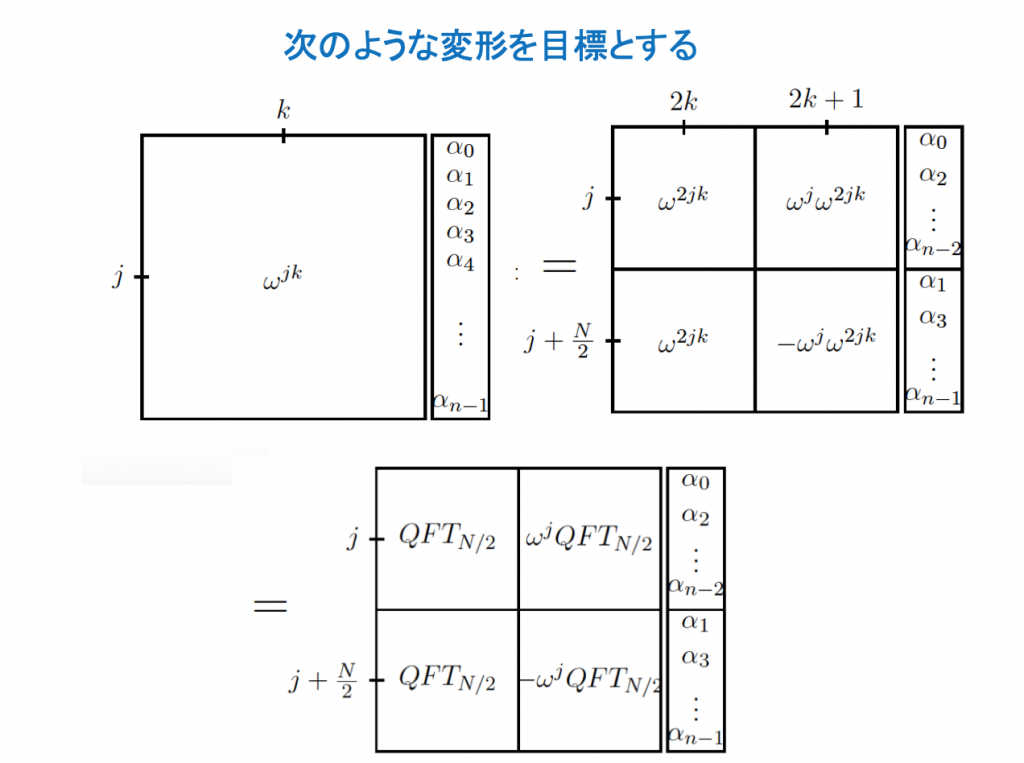
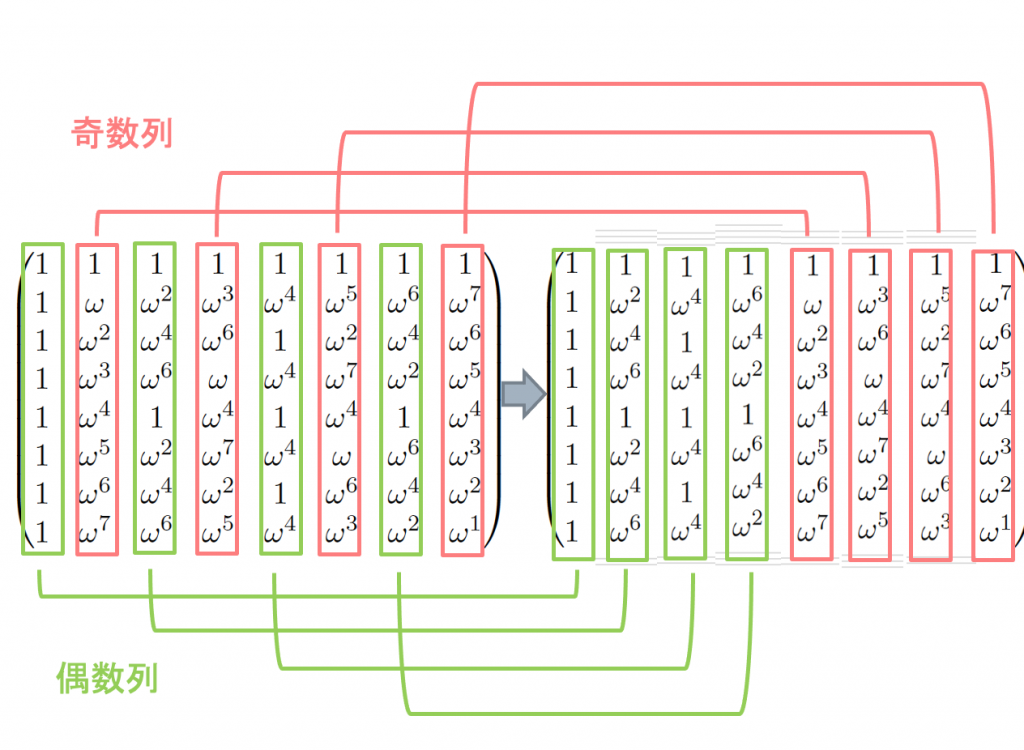
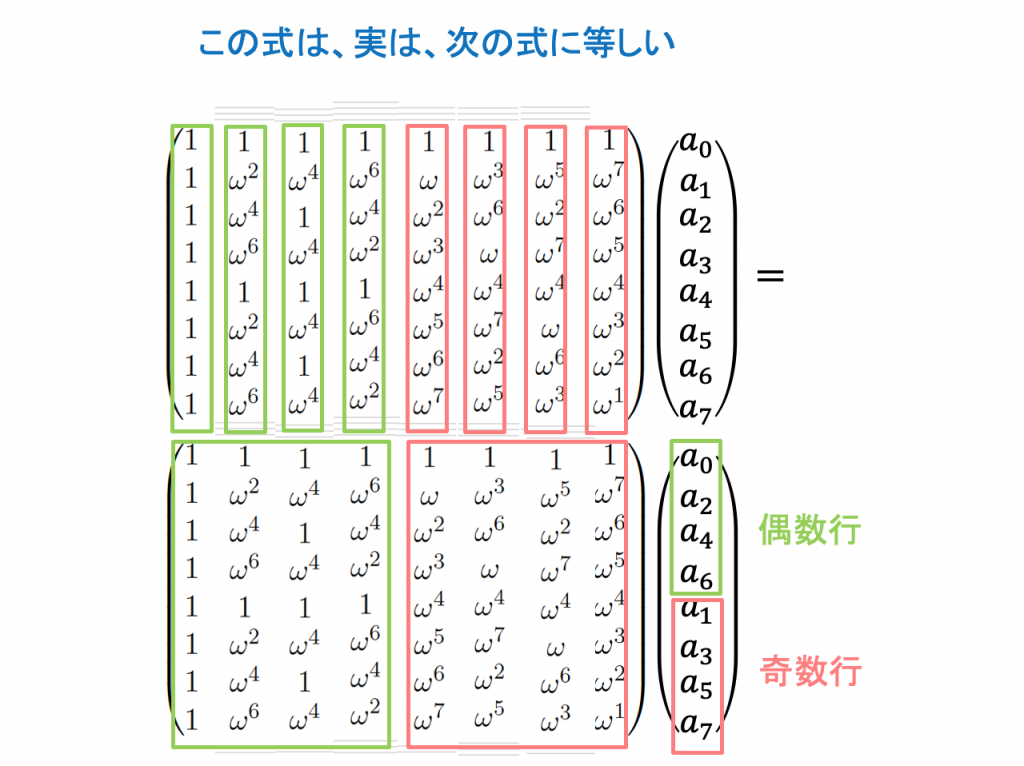
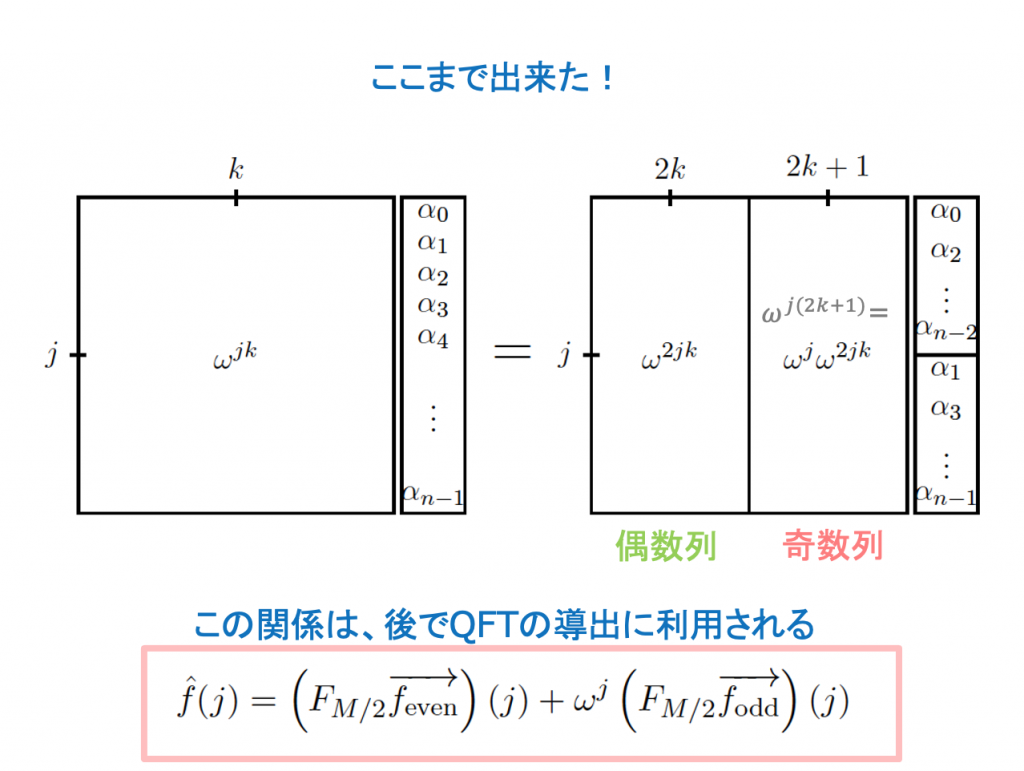
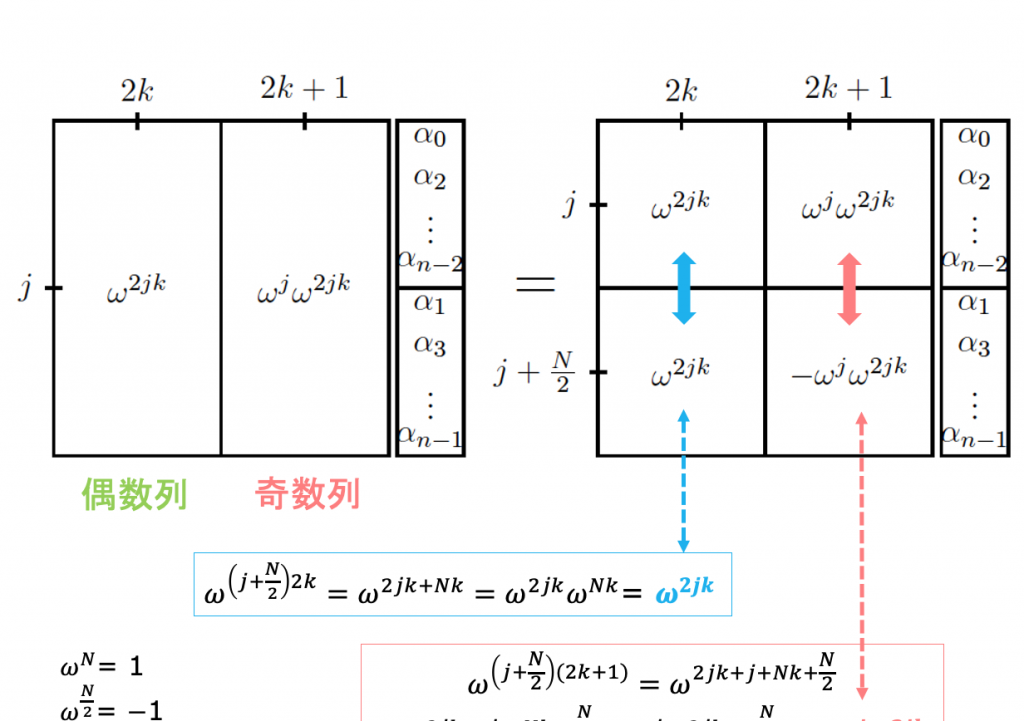
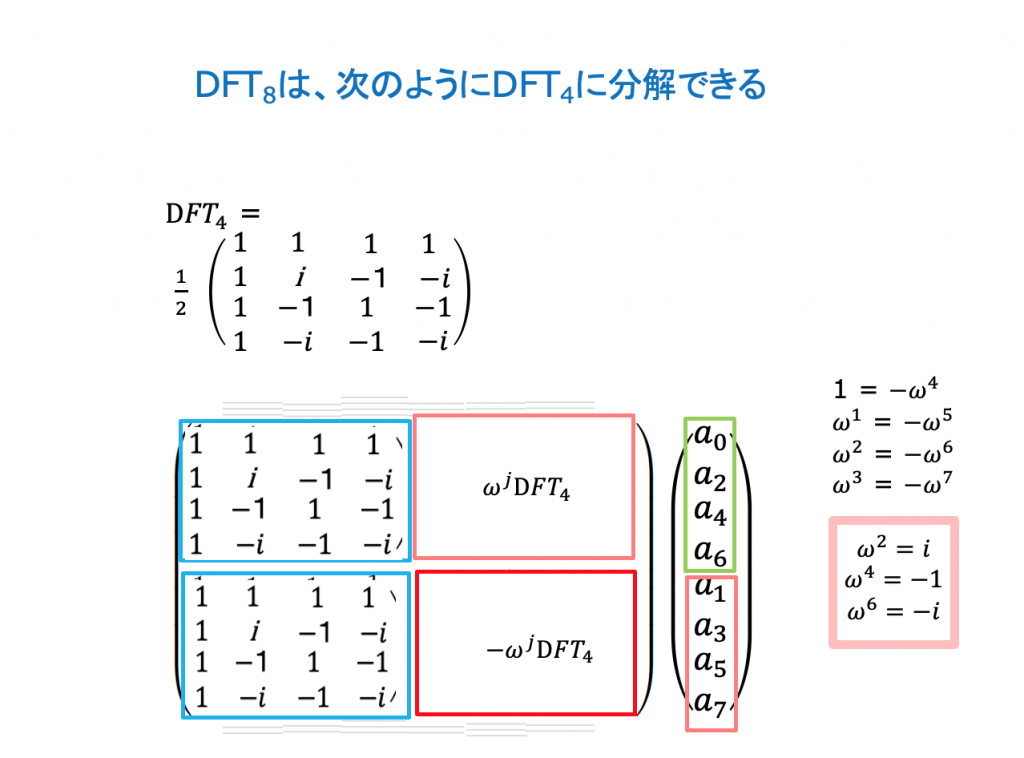
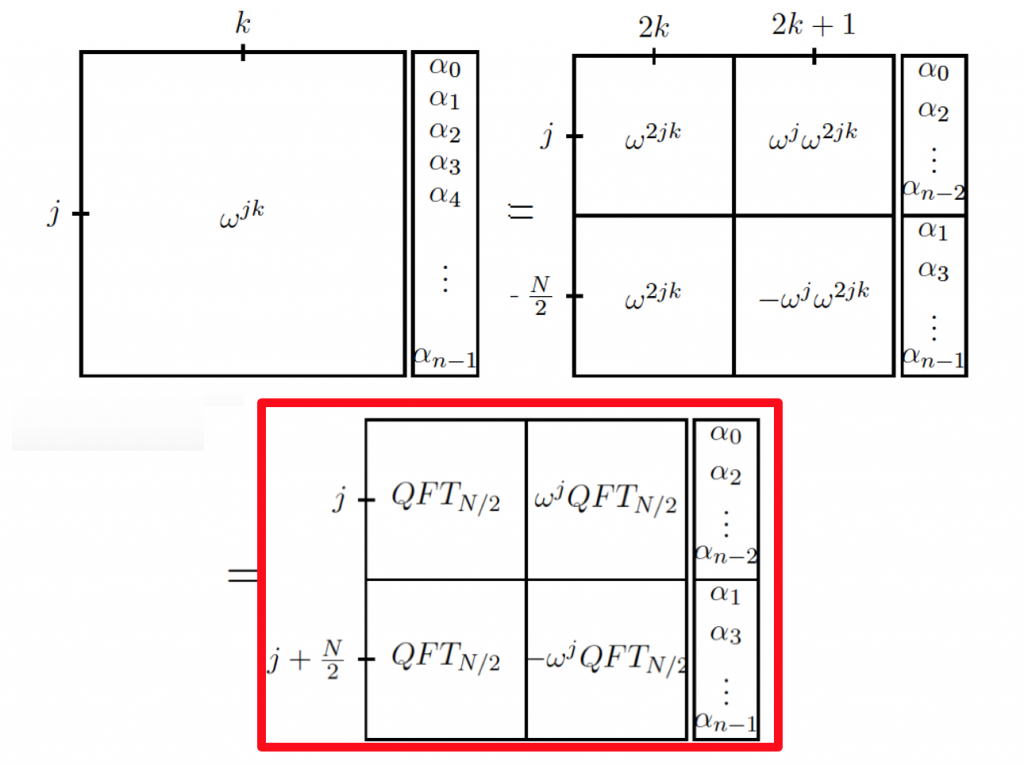
FFTでは、偶数部分と奇数部分に分け、奇数項にフェーズωjを掛けた。QFTでは、このステップは、かなり簡単になる。偶数項も奇数項も重ね合わせの状態にある。奇数項は最小bitが1の項で、奇数項は最小bitが0である。それゆえ、奇数項にも偶数項にも、QFTM-1を適用できる。
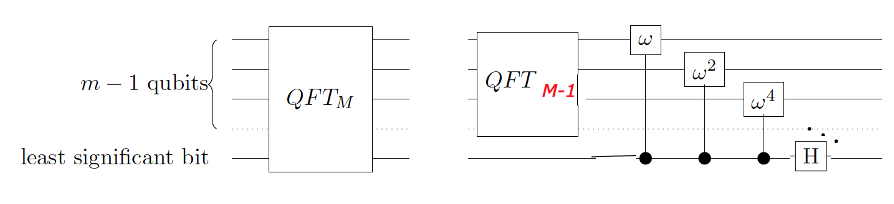
こうやればいい。単に、m-1 msb(most significant bit)にQFTM-1を適用して、lsb(least significant bit)にアダマールを適用して、再結合すればいい。

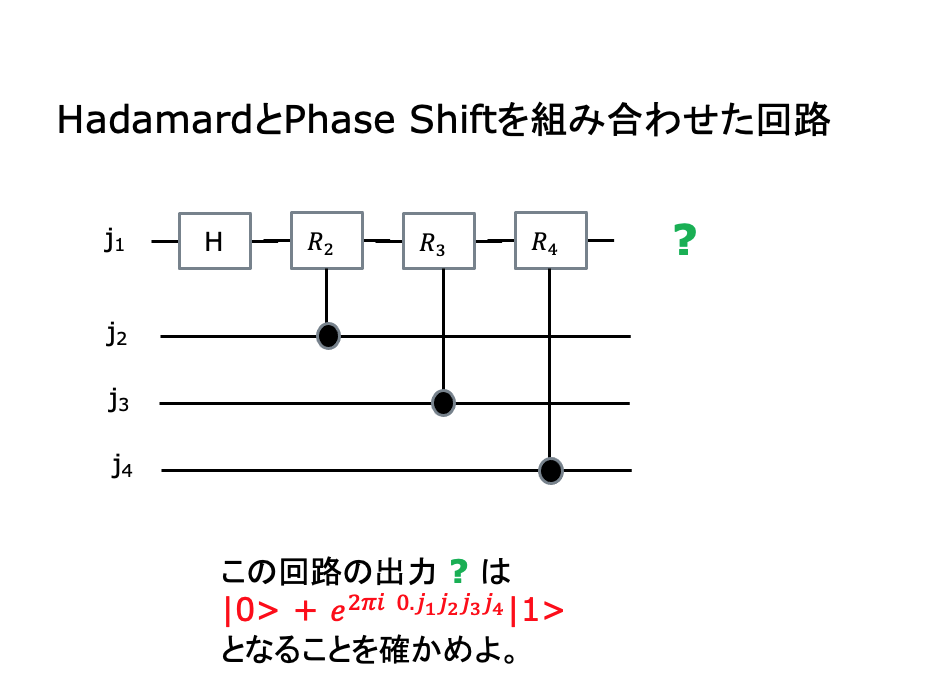
Controll Phase Shift
oフェーズをかける作用だが、それぞれの奇数項 j に、 ωj を掛ける。奇数項は最小bitが1の項で、奇数項は最小bitが0である。lsbが 1の時のみ、偶数項には何もしないように、コントロール-Phase Shiftを使う。
コントロール-Phase Shiftで利用されるフェーズωjは、k番目のbitについて言えば、 j = 2k である。
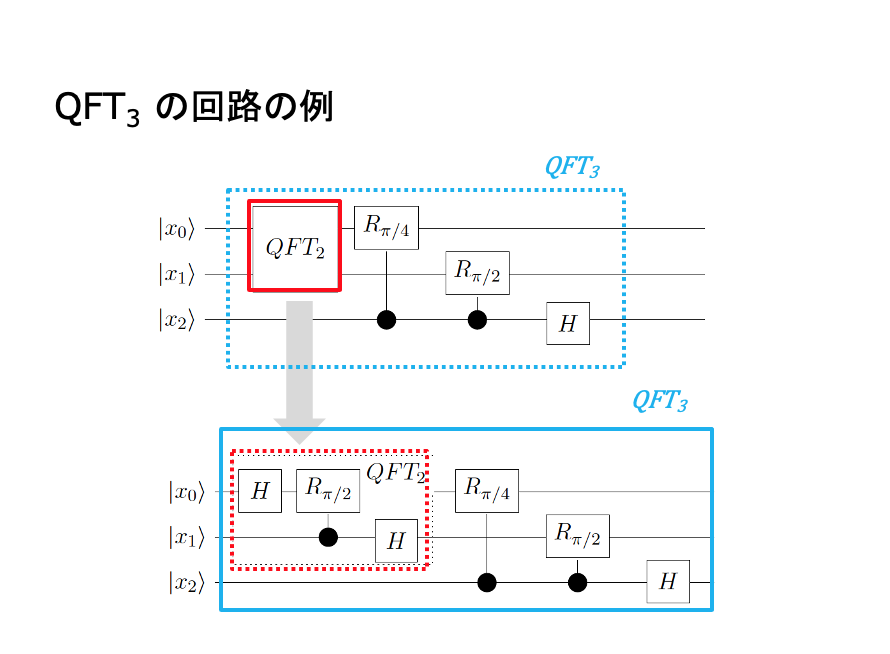
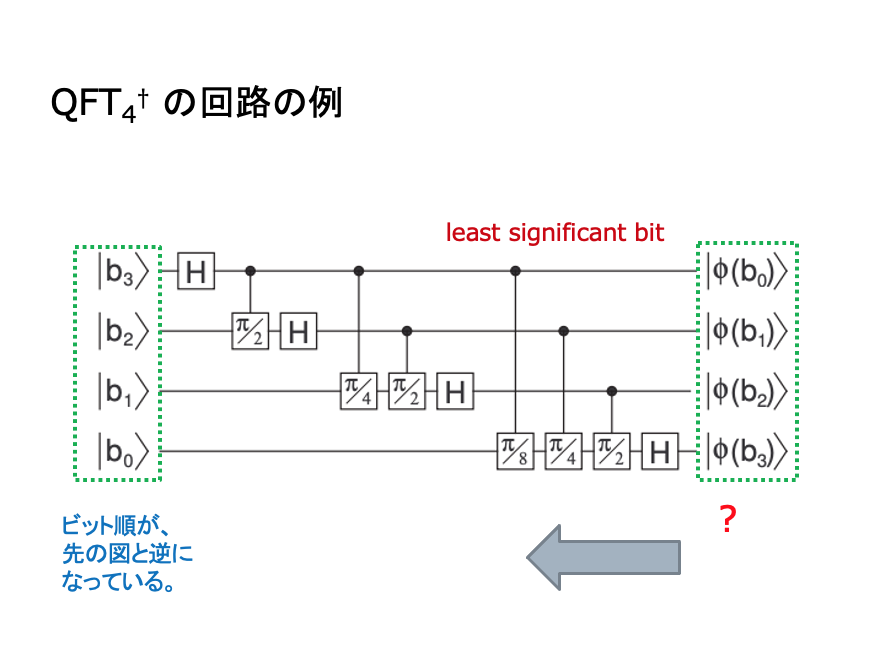
QFTの定義から、回路を導出する