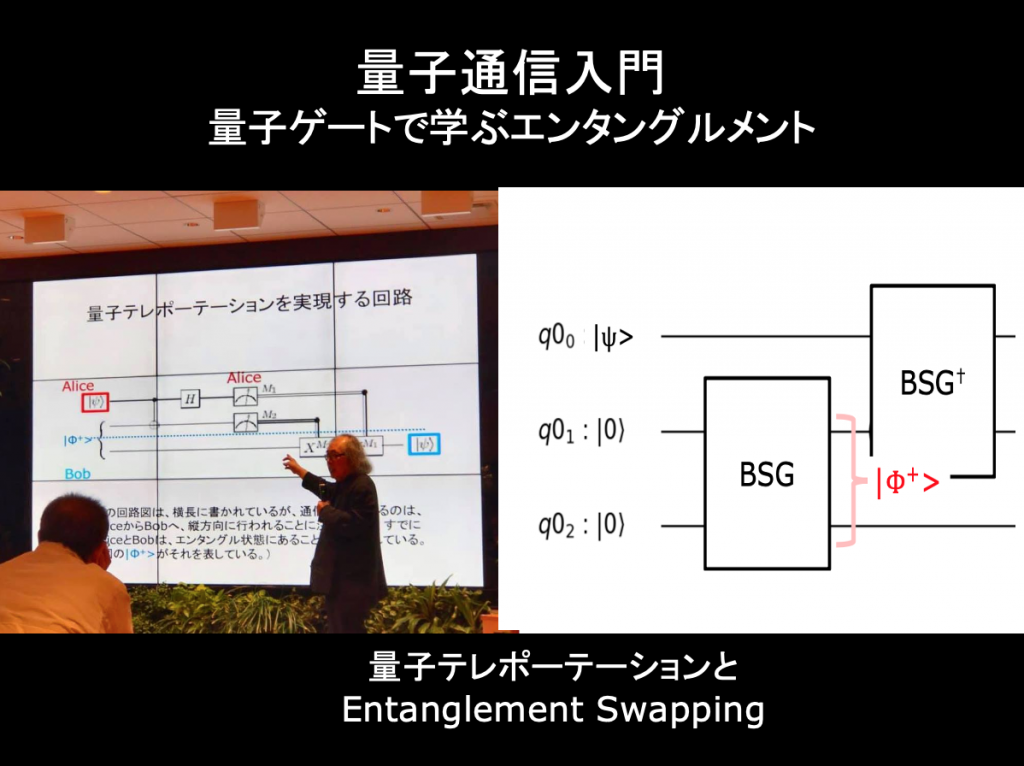
量子テレポーテーション入門 — 量子ゲートで学ぶエンタングルメント
2022年度のノーベル物理学賞について
2022年のノーベル物理学賞は、アラン・アスペ、ジョン・クラウザー、アントン・ツァイリンガーの三人に与えられました。三人は、いずれも「エンタングルメント」にかかわる実証的な実験の分野で大きな仕事をしてきた人たちです。三人のノーベル賞受賞をきっかけに、「エンタングルメント」に対する関心が多くの人の間で高まることを期待しています。
三人の仕事については、次のMaruLaboのコンテンツに詳しい説明があります。参照ください。
- 「エンタングルメントで理解する量子の世界」https://www.marulabo.net/docs/entangle-talk/
- 「量子テレポーテーション入門 — 量子ゲートで学ぶエンタングルメント」https://www.marulabo.net/docs/teleportation-2
- 「CHSHゲーム入門 — nonlocal game とInteractive Proof」https://www.marulabo.net/docs/nonlocal-game/
MaruLaboでは、「エンタングルメント」が21世紀の技術と科学の発展で中心的な役割を果たすと考えています。
次のページを参照ください。
このページは、アントン・ツァイリンガーの仕事「量子テレポーテーション」に関するものです。
「量子テレポーテーション入門」概要
なぜ、量子通信に注目するのか?
セミナーのテーマは、量子通信技術です。
量子論のITへの応用としては、もちろん、量子コンピュータ技術があるのですが、量子通信技術はそれと並ぶ重要な量子論の応用分野です。そのことは、現代のIT技術が、コンピュータ単体の技術だけではなく、コンピュータを結合するとネットワーク技術によって支えられていることを考えればわかりやすいと思います。インターネットもクラウドも、コンピュータとネットワークが結びつくことによって 実現された、技術的な飛躍でした。同じように、量子コンピュータと量子通信が結びつく未来には大きな可能性があります。
現在、量子通信技術に注目すべき理由が、いくつかあるように思います。
第一に、量子コンピュータが実際に利用されるようになるには、まだ10年単位の時間が必要だと考えられているのに対して、量子通信の実際の応用はそれより速いスピードで実現されるだろうと予想されていることがあります。現在の通信技術の中心である光通信技術は、量子通信技術と親和性が高いのです。
第二に、量子通信技術は、量子暗号化技術と結びついた時、誰にも破れない完全にセキュアな通信を保証します。その実践的な意味は大きなものがあります。その実現は、フルセットの能力を持つ量子コンピュータの完成とは独立に、その完成以前に可能です。
第三に、量子通信技術の発展が、量子コンピュータ技術に新しい刺激を与える可能性があります。量子通信の枠組みを構成するのは、エンタングルメント状態の量子を通信者の双方が共有することです。量子通信は、量子の興味深い性質であるエンタングルメントを利用しています。エンタングルメントを利用する新しい多様な量子アルゴリズムが登場する可能性があります。
今回のセミナーでは、量子通信の基本である「量子テレポーテーション」のメカニズムを、できるだけわかりやすく解説しようと思います。また、「エンタングルメント・スワッピング」という不思議な現象を紹介したいと思っています。
量子ゲートでエンタングルメントを学ぶ
今回のセミナーには、もうひとつの目的があります。それは、量子ゲートでエンタングルメントを学ぶということです。
セミナーでは、量子のエンタングルメントを、量子通信入門の出発点に置きました。具体的には、計算基底をBell基底に変換する Bell State Gateと、その逆変換である、Bell基底を計算基底に変換するBell Measure Gateを、基本的な量子通信回路 / プロトコルの説明の基礎においています。
筆者は、エンタングルメントの性質をあれこれ頭の中で考えるより、エンタングルメント状態を、具体的な量子回路上で操作する経験を積む方が、エンタングルメントの理解は深まると考えています。エンタングルメントの理解を深める上で、量子通信の基本的なプロトコルは、とてもいい素材になると考えています。
量子回路上の計算で量子通信で必須のエンタングルメント状態を扱うと言うのは、回路の個別のライン上の状態に分離できない状態を扱うと言うことです。その計算には、少しコツがいります。
基本的には、回路を特定の時刻で縦にタイムスライスして、複数のラインのテンソル積として、その時点での系の状態を計算します。系の状態は、基底のテンソル積で表現される状態の重ね合わせで表現されるので、演算子の線形性を利用すれば、基底に対する作用さえわかれば和の形に分解できるのです。
文章にすると面倒くさいのっですが、慣れれば、簡単なことです。今回のセミナーの目標の一つは、こうしたエンタングルメント状態を含んだ回路の計算に慣れてもらうことです。それは、エンタングルメントに対する理解を深めると考えています。
(2020/08/28 マルゼミ)
講演ビデオ
量子テレポーテーション入門 — 量子ゲートで学ぶエンタングルメント (1)
量子テレポーテーション入門 — 量子ゲートで学ぶエンタングルメント (2)
量子テレポーテーション入門 — 量子ゲートで学ぶエンタングルメント (3)
講演資料 (ダウンロード)
解説ビデオと解説資料pdf
Bell State を生成するBell State Gate (1)
( このビデオの解説資料pdf )
Bell State を生成するBell State Gate (2) 計算練習編
( このビデオの解説資料pdf )
Bell State を計測するBell Measure Gate (1)
( このビデオの解説資料pdf )
Bell State を計測するBell Measure Gate (2) 計算練習編
( このビデオの解説資料pdf )
Bell State GateとBell Measure Gate
( このビデオの解説資料pdf )
量子回路上での量子状態の「交換」
( このビデオの解説資料pdf )
Superdense Coding
( このビデオの解説資料pdf )
Entanglement Swapping
( このビデオの解説資料pdf )
量子テレポーテーション
( このビデオの解説資料pdf )


